Uma embalagem possui o formato de um cone. Sabendo que o raio da base desse cone é de 12 cm e sua altura é de 16 cm, então a área total dessa embalagem é:
(Use π = 3)
A) 1152 cm²
B) 1232 cm²
C) 1315 cm²
D) 1408 cm²
E) 1500 cm²
Alternativa A
Primeiro encontraremos a geratriz do cone:
g² = r² + h²
g² = 12² + 16²
g² = 144 + 256
g² = 400
g = √400
g = 20
Agora calcularemos a área total:
At = π · r (r + g)
At = 3 · 12 (12 + 20)
At = 36 ⸳ 32
At = 1152 cm²
2) Observar um cone, João fez três afirmativas:
I → O cone é um poliedro de base circular.
II → Devido à forma arredondada, o cone é um corpo redondo.
III → O cone possui a forma de um polígono.
Analisando as afirmativas feitas pelo João, podemos afirmar que:
A) Somente a I está correta.
B) Somente a II está correta.
C) Somente a III está correta.
D) Somente I e II estão corretas.
E) Somente II e III estão corretas.
alternativa B
3) (IDCAP) A figura abaixo é de um cone que tem o volume V = 37,68 cm³ e cujo raio da base é r = 3 cm. Considerando π = 3,14, a medida de g é:
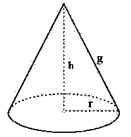
Então, a geratriz desse cone é igual a:
A) 4 cm
B) 3 cm
C) 28 cm
D) 5 cm
E) 113 cm
Então, temos que:
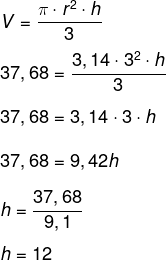
Agora sabemos que:
g² = h² + r²
g² = 4² + 3²
g² = 16 + 9
g² = 25
g = √25
g = 5
4)(Enem – PPL) Um arquiteto está fazendo um projeto de iluminação de ambiente e necessita saber a altura que deverá instalar a luminária ilustrada na figura.
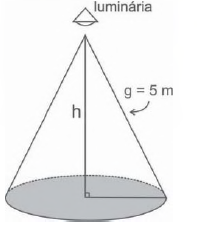
Sabendo que a luminária deverá iluminar uma área circular de 28,26 m², considerando π ≅ 3,14, a altura h será igual a
A) 3 m.
B) 4 m.
C) 5 m.
D) 9 m.
E) 16 m.
Alternativa B
Sabemos que:
A = π ⸳ r²
Calculando o raio, temos que:
28,26 = 3,14 . r²
r² = 28,26 : 3,14
r² = 9
r = √9
r = 3 metros
Agora, encontraremos a altura, pois sabemos que:
g² = h² + r²
5² = h² + 3²
25 = h² + 9
25 – 9 = h²
h² = 16
h = √16
h = 4 metros



Nenhum comentário:
Postar um comentário