Jogos Matemáticos parte 1

Jogos Matemáticos.Matemática não dói!!!!!!!!!!!

Números positivos e negativos, equações e figuras geométricas. Nem todos os alunos
consideram o estudo da matemática um pesadelo. Em algumas escolas, as aulas dessa disciplina - que já assustou muitos estudantes - tem se tornado momentos de descobertas e diversão. O quadro-negro cedeu espaço a jogos de todos os tipos que desafiam meninos e meninas de várias idades. O que começa com uma simples competição entre os colegas, termina ensinando
conceitos e formas deferentes de raciocínio.

Na escola da serra, não existe problema matemático que seja difícil demais para os alunos. "gosto de todos os conteúdos e, principalmente, de somar. Não me lembro de ter estudado nenhumamatéria difícil", explica Paula Resende, de 6 anos. Para Letícia Rocha, de sete, aprender jogando é mais fácil. "Durante os jogos, temos que pensar bastante e fazer várias contas", explica. Ubiratan Machado, também de sete, acredita que os jogos facilita o aprendizado, tornando-o mais divertido. 'A gente joga e só depois percebe que está aprendendo", descreve Bruno Vilela , de sete.

Os professores defendem o uso de novos recursos para o ensino da disciplina.
"Ao participar das competições, o aluno vai descobrindo os conceitos e registrando os resultados
no caderno. Não basta dizer a resposta certa, é preciso descrever que raciocínio foi adotado", explica a professora do 1º ano do 1º ciclo da Escola da Serra, Denise Vitarelli. A professora
Maguy Sales, que dá aula para a mesma série, lembra que as aulas tradicionais são mais fáceis.
"Se a proposta é diferenciada, a aula tem outro ritmo", afirma. (FR)

Pouco a pouco, a estratégia de utilizar jogos no ensino da matemática vem conquistando adeptos.
Em breve, as competições matemáticas devem chegar as escolas públicas. Na PUC-Betim, os estudantes do curso de matemática trabalham durante vários períodos na criação de jogos pedagógicos, que facilitam o ensino da disciplina.

A proposta foi tão bem sucedida que deve ser implantada em algumas escolas pública do município. "Investigamos quis o recursos didáticos existente para o ensino da geometria para estudantes
cegos. Criamos uma caixa de madeira, onde o aluno pode aprender sobre ângulo, triângulo, circunferência, raio, funções e gráfico. Fizemos alterações na caixa e descobrimos que ela serve para
ensinar geometria a qualquer estudante", descreve a aluna do 7º período do curso de matemática, Poliana Januário, que desenvolve
o projeto com outros cinco colegas.
Outro grupo, do 5º período do mesmo curso, desenvolveu os jogos laranja na cesta e corridas de carro para ensinar os conteúdos de matemática a alunos á partir dos quatro anos. " O aluno joga
um dado que determina quantas laranjas tem que ser retirada da cesta. Ele aprende sobre quantidades e a fazer somas e subtrações", explica Ângela Maria Ribeiro, que desenvolveu o projeto em parceria com Lorena Darós Silva. Na corrida, o aluno só tem autorização para
avançar com seu carro se acertar a pergunta feita pela professora. " Para o aluno, o jogo é uma forma de visualizar o conteúdo aprendido", detalha Ângela. (FR)

O Departamento de Matemática da UFMG tem um laboratório cheio de jogos matemáticos.
Todos os meses, a Universidade recebe alunos de várias escolas. - públicas e particulares - para
uma aula diferente e mais divertida. "A escola fornece a idade dos alunos e montamos a visita. Todos os jogos são montados com materiais baratos. Ou seja, o professor pode levar a
experiência para dentro de sala. Pelos jogos, identificamos que linguagem os alunos utilizam para aprender. A participação nas aulas é muito boa", explica a coordenadora do projetos Visitas Programadas ao Laboratório de Ensino de Matemática da UFMG, Maria Cristina Costa Ferreira. Ela afirma que não é possível ensinar toda a matemática apenas pelos jogos. "Há um momento
que precisamos fazer a síntese do que foi ensinado, orienta.

Os alunos aprovam as inovações. "É bem melhor aprender assim. A gente aprende quando copia
do quadro, mas não é tão divertido", afirma Ana Cristina Landó, de 11 anos, estudante da 6ª série
do Centro Pedagógico da UFMG. Para Matheus Lima, , de 12, da mesma sala, o jogo exige que
o aluno se dedique mais ao aprendizado.

"A gente aprende muito mais. No jogo somos pressionado e precisamos nos esforçar para dar a resposta", diz Gustavo Aleixo, de 12. Já Rafaela Bessone, de 12, acredita que o jogo traz mais desafios, chamando a atenção dos alunos.. "O jogo é difícil. Só que aprender copiando a matéria
no quadro é pior. Assim fica mais interessante", comenta Gabriela Torrésia Lima, da mesma idade. Maria Cristina afirma que, a matemática está sendo ensinada de forma mais contextualizada.
"Em muitas escolas, os conteúdos são vistos juntos com outras matérias. Isso aumenta o prazer
da aprendizagem", defende.(FR)

Trilha

Os próprios alunos criam um tabuleiro, com os obstáculos e a história. O jogo ensina seqüência numérica, ordem crescente e decrescente, contagem e quantificação.

Bingo

Nas cartelas tradicionais, o aluno aprende a ler os números. Durante o sorteio, o professor pode anunciar os números de forma diferenciada, falando sobre dezenas, unidades,antecessores e sucessores, ou exigindo algum tipo de operação para a descoberta do numero sorteado.

Batalha Dupla

Cada aluno retira duas cartas de um baralho tradicional. Elas devem ser somadas ou subtraídas, conforme a orientação do professor. Quem tiver o maior resultado ganha a carta do colega.
Vence o jogo quem tiver mais pontos, somados no final da competição.

Atrás da Orelha

O jogo tem dois jogadores e um juiz. Os jogadores retiram uma carta do baralho, sem ver qual é o seu número. A carta deve ser colocada atrás da orelha para que apenas o outro jogador veja seu número. Cabe ao juiz dizer qual o resultado da soma ou da subtração das duas cartas. Para vencer, o jogador vê a carta do colega e precisa raciocinar para descobrir qual é a sua.

Poliminó

É uma espécie de quebra-cabeça formado por várias figuras geométricas, criadas á partir de monominós, que são unidades-padrão. Para montar o poliminó, o aluno precisa pensar no conceito de área e perímetro de uma figura plana.

Torre de Hanói

Jogo milenar que utiliza um tabuleiro de madeira, com pequenas torres e aros de diversos
tamanhos. Para vencer o desafio - que pode ser o tempo gasto para colocar aros em determina ordem nas torres - o aluno faz estimativas e raciocina sobre múltiplos, potências e equações.
O jogo serve também para organizar o pensamento.

Poli cubos

O jogo é semelhante ao poliminó, mas o quebra-cabeça é uma espécie de cubo. Nesse jogo, o
aluno estuda o volume das figuras.

Corrida Algébrica

Na corrida algébrica, o aluno vai avançar com seu pino no tabuleiro depois de descobrir qual é o resultado de uma equação. O próprio aluno pode escolher que valor deseja atribuir á variável,
de forma a conseguir o resultado maior.

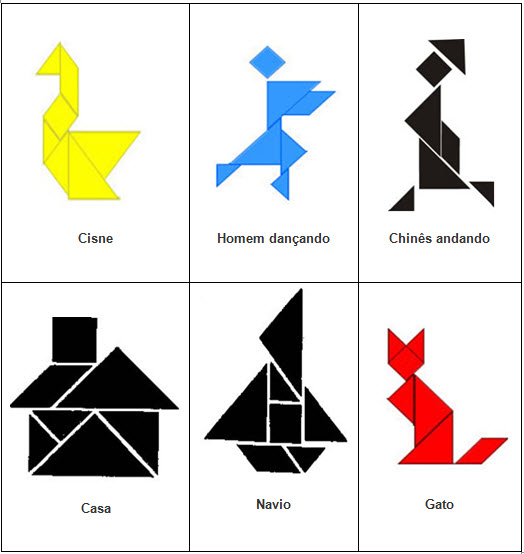
Tangran

O jogo tem várias peças, com tamanhos variados. O aluno estuda área, polígono, perímetro e
até frações.

Jogo da Estrela

Cada aluno retira um número positivo ou negativo do tabuleiro. Vence quem obter o maior
resultado, depois de fazer a soma dos números escolhidos. Nesse jogo, os estudantes aprendem
a soma dos números negativos e positivos, ordem e conceito de oposto.


(Reportagem extraída do Jornal "Estado de Minas" de 05 de abril de 2003 - Caderno Gurilândia)

SIMULADO 04 - Raciocínio lógico com gabarito

1) Sabe-se que existe pelo menos um A que é B. Sabe-se, também, que todo B é C. Segue-se,

portanto, necessariamente que

a) todo C é B

b) todo C é A

c) algum A é C

d) nada que não seja C é A

e) algum A não é C

2) Considere as seguintes premissas (onde X, Y, Z e P são conjuntos não vazios):

Premissa 1: "X está contido em Y e em Z, ou X está contido em P"

Premissa 2: "X não está contido em P"

Pode-se, então, concluir que, necessariamente

a) Y está contido em Z

b) X está contido em Z

c) Y está contido em Z ou em P

d) X não está contido nem em P nem em Y

e) X não está contido nem em Y e nem em Z

3) Três rapazes e duas moças vão ao cinema e desejam sentar-se, os cinco, lado a lado, na

mesma fila. O número de maneiras pelas quais eles podem distribuir-se nos assentos de modo que as duas moças fiquem juntas, uma ao lado da outra, é igual a

a) 2

b) 4

c) 24

d) 48

e) 120

4) De um grupo de 200 estudantes, 80 estão matriculados em Francês, 110 em Inglês e 40 não estão matriculados nem em Inglês nem em Francês. Seleciona-se, ao acaso, um dos 200 estudantes. A probabilidade de que o estudante selecionado esteja matriculado em pelo menos uma dessas disciplinas (isto é, em Inglês ou em Francês) é igual a

a) 30/200

b) 130/200

c) 150/200

d) 160/200

e) 190/200

5) Uma herança constituída de barras de ouro foi totalmente dividida entre três irmãs: Ana, Beatriz e Camile. Ana, por ser a mais velha, recebeu a metade das barras de ouro, e mais meia barra. Após Ana ter recebido sua parte, Beatriz recebeu a metade do que sobrou, e mais meia barra. Coube a Camile o restante da herança, igual a uma barra e meia. Assim, o número de barras de ouro que Ana recebeu foi:

a) 1

b) 2

c) 3

d) 4

e) 5

6) Chama-se tautologia a toda proposição que é sempre verdadeira, independentemente da

verdade dos termos que a compõem. Um exemplo de tautologia é:

a) se João é alto, então João é alto ou Guilherme é gordo

b) se João é alto, então João é alto e Guilherme é gordo

c) se João é alto ou Guilherme é gordo, então Guilherme é gordo

d) se João é alto ou Guilherme é gordo, então João é alto e Guilherme é gordo

e) se João é alto ou não é alto, então Guilherme é gordo

7) Sabe-se que a ocorrência de B é condição necessária para a ocorrência de C e condição

suficiente para a ocorrência de D. Sabe-se, também, que a ocorrência de D é condição necessária e suficiente para a ocorrência de A. Assim, quando C ocorre,

a) D ocorre e B não ocorre

b) D não ocorre ou A não ocorre

c) B e A ocorrem

d) nem B nem D ocorrem

e) B não ocorre ou A não ocorre

8) Se Frederico é francês, então Alberto não é alemão. Ou Alberto é alemão, ou Egídio é

espanhol. Se Pedro não é português, então Frederico é francês. Ora, nem Egídio é espanhol nem Isaura é italiana. Logo:

a) Pedro é português e Frederico é francês

b) Pedro é português e Alberto é alemão

c) Pedro não é português e Alberto é alemão

d) Egídio é espanhol ou Frederico é francês

e) Se Alberto é alemão, Frederico é francês

9) Se Luís estuda História, então Pedro estuda Matemática. Se Helena estuda Filosofia, então Jorge estuda Medicina. Ora, Luís estuda História ou Helena estuda Filosofia. Logo, segue-se necessariamente que:

a) Pedro estuda Matemática ou Jorge estuda Medicina

b) Pedro estuda Matemática e Jorge estuda Medicina

c) Se Luís não estuda História, então Jorge não estuda Medicina

d) Helena estuda Filosofia e Pedro estuda Matemática

e) Pedro estuda Matemática ou Helena não estuda Filosofia

10) Maria tem três carros:

um Gol, um Corsa e um Fiesta.

Um dos carros é branco, o outro é preto, e o outro é azul.

Sabe-se que:

1) ou o Gol é branco, ou o Fiesta é branco,

2) ou o Gol é preto, ou o Corsa é azul,

3) ou o Fiesta é azul, ou o Corsa é azul,

4) ou o Corsa é preto, ou o Fiesta é preto. Portanto, as cores do Gol, do Corsa e do Fiesta são, respectivamente,

a) branco, preto, azul

b) preto, azul, branco

c) azul, branco, preto

d) preto, branco, azul

e) branco, azul, preto

GABARITO

1) C

2) B

3) D

4) D

5) E

6) A

7) C

8) B

9) A

10) E

( fonte: http://www.ebah.com.br/)

SIMULADO 03 - Raciocínio Lógico Matemático com gabarito

SIMULADO 03 - Raciocínio Lógico Matemático com gabarito

01 (ESAF/AFTN/96) - Três amigas, Tânia, Janete e Angélica, estão sentadas lado a lado em um teatro. Tânia sempre fala a verdade; Janete às vezes fala a verdade; Angélica nunca fala a verdade. A que está sentada à esquerda diz: "Tânia é quem está sentada no meio". A que está sentada no meio diz: "Eu sou Janete". Finalmente, a que está sentada à direita diz: "Angélica é quem está sentada no meio". A que está sentada à esquerda, a que está sentada no meio e a que está sentada à direita são, respectivamente:

1. Janete, Tânia e Angélica
2. Janete, Angélica e Tânia
3. Angélica, Janete e Tânia
4. Angélica, Tânia e Janete
5. Tânia, Angélica e Janete

02 (ESAF/AFTN/96) - José quer ir ao cinema assistir ao filme "Fogo contra Fogo" , mas não tem certeza se o mesmo está sendo exibido. Seus amigos, Maria, Luís e Júlio têm opiniões discordantes sobre se o filme está ou não em cartaz. Se Maria estiver certa, então Júlio está enganado. Se Júlio estiver enganado, então Luís está enganado. Se Luís estiver enganado, então o filme não está sendo exibido. Ora, ou o filme "Fogo contra Fogo" está sendo exibido, ou José não irá ao cinema. Verificou-se que Maria está certa. Logo:

o filme "Fogo contra Fogo" está sendo exibido

1. Luís e Júlio não estão enganados
2. Júlio está enganado, mas não Luís
3. Luís está engando, mas não Júlio
4. José não irá ao cinema

03 (ESAF/AFTN/96) - De todos os empregados de uma grande empresa, 30% optaram por realizar um curso de especialização. Essa empresa tem sua matriz localizada na capital. Possui, também, dua filiais, uma em Ouro Preto e outra em Montes Claros. Na matriz trabalham 45% dos empregados e na filial de Ouro Preto trabalham 20% dos empregados. sabendo-se que 20% dos empregados da capital optaram pela realização do curso e que 35% dos empregados da filial de Ouro Preto também o fizeram, então a percentagem dos empregados da filial de Montes Claros que não optaram pelo curso é igual a:

1. 60%
2. 40%
3. 35%
4. 21%
5. 14%

04 (ESAF/AFTN/96) - Se Nestor disse a verdade, Júlia e Raul mentiram. Se Raul mentiu, Lauro falou a verdade. Se Lauro falou a verdade, há um leão feroz nesta sala. Ora, não há um leão feroz nesta sala. Logo:

1. Nestor e Júlia disseram a verdade
2. Nestor e Lauro mentiram
3. Raul e Lauro mentiram
4. Raul mentiu ou Lauro disse a verdade
5. Raul e Júlia mentiram

05 (ESAF/AFTN/96) - Os carros de Artur, Bernardo e Cesar são, não necessariamente nesta ordem, uma Brasília, uma Parati e um Santana. Um dos carros é cinza, um outro é verde, e o outro é azul. O carro de artur é cinza; o carro de Cesar é o Santana; o carro de Bernardo não é verde e não é a Brasília. As cores da Brasília, da Parati e do Santana são, respectivamente:

1. cinza, verde e azul
2. azul, cinza e verde
3. azul, verde e cinza
4. cinza, azul e verde
5. verde, azul e cinza

06 (ESAF/AFTN/96) - Sabe-se que na equipe do X Futebol Clube (XFC) há um atacante que sempre mente, um zagueiro que sempre fala a verdade e um meio-campista que às vezes fala a verdade e às vezes mente. Na saída do estádio, dirigindo-se a um torcedor que não sabia o resultado do jogo que terminara, um deles declarou "Foi empate", o segundo disse "Não foi empate" e o terceiro falou "Nós perdemos". O torcedor reconheceu somente o meio-campista mas pôde deduzir o resultado do jogo com certeza. A declaração do meio-campista e o resultado do jogo foram, respectivamente:

1. "Foi empate"/ o XFC venceu
2. "Não foi empate"/ empate
3. "Nós perdemos / o XFC perdeu
4. "Não foi empate" / o XFC perdeu
5. "Foi empate" / empate

07 (ESAF/AFTN/96) - Em um laboratório de experiências veterinárias foi observado que o tempo requerido para um coelho percorrer um labirinto, na enésima tentativa, era dado pela função C(n) = (3+12/n) minutos. Com relação a essa experiência pode-se afirmar, então, que um coelho:

1. consegue percorrer o labirinto em menos de três minutos
2. gasta cinco minutos e quarenta segundos para percorrer o labirinto na quinta tentativa
3. gasta oito minutos para percorrer o labirinto na terceira tentativa
4. percorre o labirinto em quatro minutos na décima tentativa
5. percorre o labirinto numa das tentativas, em três minutos e trinta segundos

08 (ESAF/AFTN/96) - O salário mensal de um vendedor é constituído de uma parte fixa igual a R$ 2.300,00 e mais uma comissão de 3% sobre o total de vendas que exceder a R$ 10.000,00. Calcula-se em 10% o percentual de descontos diversos que incidem sobre seu salário bruto. Em dois meses consecutivos, o vendedor recebeu, líquido, respectivamente, R$ 4.500,00 e R$ 5.310,00. Com esses dados, pode-se afirmar que suas vendas no segundo mês foram superiores às do primeiro mês em:

1. 18%
2. 20%
3. 30%
4. 33%
5. 41%

09 (ESAF/AFTN/96) - Em determinado país existem dois tipos de poços de petróleo, Pa e Pb. Sabe-se que oito poços Pa mais seis poços Pb produzem em dez dias tantos barris quanto seis poços Pa mais dez poços Pb produzem em oito dias. A produção do poço Pa, portanto, é:

1. 60,0% da produção do poço Pb
2. 60,0% maior do que a produção do poço Pb
3. 62,5% da produção do poço Pb
4. 62,5% maior do que a produção do poço Pb
5. 75,0% da produção do poço Pb

10 (ESAF/AFTN/96) - Uma ferrovia será construída para ligar duas cidades C1 eC2, sendo que esta última localiza-se a vinte quilômetros ao sul de C1. No entanto, entre essas duas cidades, existe uma grande lagoa que impede a construção da ferrovia em linha reta. Para contornar a lagoa, a estrada deverá ser feita em dois trechos, passando pela cidade C3, que está a dezesseis quilômetros a leste e dezoito quilômetros ao sul de C1. O comprimento, em quilômetros, do trecho entre a cidade C3 e a cidade C2 é igual a:

1. 2 / Ö 5
2. Ö 5 / 2
3. 4 / Ö 5
4. 2 Ö 5
5. 4 Ö 5

11 (ESAF/AFTN/98) - Considere as afirmações: A) se Patrícia é uma boa amiga, Vítor diz a verdade; B) se Vítor diz a verdade, Helena não é uma boa amiga; C) se Helena não é uma boa amiga, Patrícia é uma boa amiga. A análise do encadeamento lógico dessas três afirmações permite concluir que elas:

a) implicam necessariamente que Patrícia é uma boa amiga

b) são consistentes entre si, quer Patrícia seja uma boa amiga, quer Patrícia não seja uma boa amiga

c) implicam necessariamente que Vítor diz a verdade e que Helena não é uma boa amiga

d) são equivalentes a dizer que Patrícia é uma boa amiga

e) são inconsistentes entre si

12 (ESAF/AFTN/98) - Indique qual das opções abaixo é verdadeira.

a) Para algum número real x, tem-se que x < 4 e que x2 + 5x = 0

b) Para todo número real y, tem-se que y < 3 e que y > 2

c) Para todo número real positivo x, tem-se que x2 > x

d) Para algum número real k, tem-se que k > 5 e que k2 – 5k = 0

e) Para algum número real x, tem-se que x < 4 e que x > 5

13 (ESAF/AFTN/98) - O valor de y para o qual a expressão trigonométrica:

(cosx + senx)2 + y senx cosx - 1 = 0

representa uma identidade é:

a) 0

b) -2

c) -1

d) 2

e) 1

15 (ESAF/AFTN/98) - Há três suspeitos de um crime: o cozinheiro, a governanta e o mordomo. Sabe-se que o crime foi efetivamente cometido por um ou por mais de um deles, já que podem ter agido individualmente ou não. Sabe-se, ainda, que: A) se o cozinheiro é inocente, então a governanta é culpada; B) ou o mordomo é culpado ou a governanta é culpada, mas não os dois; C) o mordomo não é inocente. Logo:

a) a governanta e o mordomo são os culpados

b) somente o cozinheiro é inocente

c) somente a governanta é culpada

d) somente o mordomo é culpado

e) o cozinheiro e o mordomo são os culpados

16 (ESAF/AFTN/98) - Em uma cidade, 10% das pessoas possuem carro importado. Dez pessoas dessa cidade são selecionadas, ao acaso e com reposição. A probabilidade de que exatamente 7 das pessoas selecionadas possuam carro importado é:

a) 120 (0,1)7 (0,9)3

b) (0,1)3 (0,9)7

c) 120 (0,1)7 (0,9)

d) 120 (0,1) (0,9)7

e) (0,1)7 (0,9)3

17 (ESAF/AFTN/98) - Uma empresa possui 20 funcionários, dos quais 10 são homens e 10 são mulheres. Desse modo, o número de comissões de 5 pessoas que se pode formar com 3 homens e 2 mulheres é:

a) 1650

b) 165

c) 5830

d) 5400

e) 5600

18 (ESAF/AFTN/98) - Sejam três retas: a reta R1 que é a bissetriz do primeiro quadrante; a reta R2 que é a bissetriz do quarto quadrante e a reta R3 que é dada pela equação x = 1. A área, em cm2, do triângulo cujos lados coincidem com essas três retas é:

a) 1,5

b) 0,5

c) 1

d) 2

e) 2,5

19 (ESAF/AFTN/98) - Em um triângulo retângulo, um dos catetos forma com a hipotenusa um ângulo de 450. Sendo a área do triângulo igual a 8 cm2, então a soma das medidas dos catetos é igual a:

a) 8 cm2

b) 4 cm

c) 8 cm

d) 16 cm2

e) 16 cm

20- Um trapézio ABCD possui base maior igual a 20 cm, base menor igual a 8 cm e altura igual a 15 cm. Assim, a altura, em cm, do triângulo limitado pela base menor e o prolongamento dos lados não paralelos do trapézio é igual a:

a) 7

b) 5

c) 17

d) 10

e) 12

GABARITO

01-B	11-B
02-E	12-A
03-A	13-B
04-B
05-D	15-E
06-A	16-A
07-E	17-D
08-C	18-C
09-C	19-C
10-D	20-D

( fonte:http://www.ebah.com.br/content)