A equação do segundo grau ou equação quadrática, recebe esse nome na medida que demostra uma equação polinomial de grau dois, cujo termo de maior grau está elevado ao quadrado; são representadas sob a forma:
ax2 + bx + c = 0
Donde x é a incógnita (termo variável), a, b e c são números reais e coeficientes da equação, sendo “a” um valor diferente de 0 (a ≠ 0).
Fórmula de Bhaskara
Observe que a equação de segundo grau busca encontrar valores reais, denominados de raiz da equação e a “Fórmula de Bhaskara” representa a fórmula geral para resolução da equação do segundo grau, uma vez que determina as raízes (valores) de uma equação quadrática:
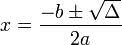
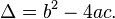
O discriminante da equação designa a letra grega delta (Δ) que equivale à expressão valor b2-4ac. Importante ressaltar que se o valor de Δ for maior que zero (Δ> 0), a equação terá duas raízes reais e distintas; se Δ for igual a zero (Δ=0), a equação apresentará somente uma raiz; e se Δ for menor que zero (Δ<0), a equação não apresentará raízes reais.
1) Exemplo: 3x²-7x+2=0
a=3, b=-7 e c=2
Delta = (-7)²-4.3.2 = 49-24 = 25
Exercícios:
1)Calcular a, b, c e delta nas equações:
a) x² + 9 x + 8 = 0
b) 9 x² - 24 x + 16 = 0
c) x² - 2 x + 4 = 0
d) 3 x² - 15 x + 12 = 0
e) x² + 6 x + 9 = 0
f) 2 x² - 2 x - 12 = 0
(R:a) a=1,b=9,c=8, delta=49 b)a=9, b=-24, c=16 e delta=0 c)a=1, b=-2, c=4 e delta=-14 d)a=3, b=-15, c=12 e delta=81 e)a=1, b=6, c=9 e delta=0 f)a=2, b=-2, c=-12 e delta=100)
2)Preencher a tabela com os coeficientes e o discriminante de cada equação do segundo grau, analisando os tipos de raízes da equação.
| Equação | a | b | c | Delta | Tipos de raízes |
|---|---|---|---|---|---|
| x²-6x+8=0 | 1 | -6 | 8 | 4 | reais e diferentes |
| x²-10x+25=0 | |||||
| x²+2x+7=0 | |||||
| x²+2x+1=0 | |||||
| x²+2x=0 |
Utilizando a fórmula de Bháskara, vamos resolver alguns exercícios:
3) RESOLVA AS EQUAÇÕES DE 2º GRAU
1) x² - 5x + 6 = 0 _____(R:2,3)
2) x² - 8x + 12 = 0 ______(R:2,6)
3) x² + 2x - 8 = 0______ (R:2,-4)
4) x² - 5x + 8 = 0 ______(R:vazio)
5) 2x² - 8x + 8 = 0_______ (R:2,)
6) x² - 4x - 5 = 0_______ (R:-1, 5)
7) -x² + x + 12 = 0_______ (R:-3, 4)
8) -x² + 6x - 5 = 0_______ (R:1,5)
9) 6x² + x - 1 = 0______ (R:1/3 , -1/2)
10) 3x² - 7x + 2 = 0 ______(R:2, 1/3)
11) 2x² - 7x = 15 _______(R:5, -3/2)
12) 4x² + 9 = 12x______ (R:3/2)
13) x² = x + 12 ______(R:-3 , 4)
14) 2x² = -12x - 18 _____(R:-3 )
15) x² + 9 = 4x_____ (R: vazio)
16) 25x² = 20x – 4 ____(R: 2/5)
17) 2x = 15 – x² ______(R: 3 , -5)
18) x² + 3x – 6 = -8____ (R:-1 , -2)
19) x² + x – 7 = 5 ____(R: -4 , 3)
20) 4x² - x + 1 = x + 3x² ___(R: 1)
21) 3x² + 5x = -x – 9 + 2x²____ (R: -3)
22) 4 + x ( x - 4) = x _____(R: 1,4)
23) x ( x + 3) – 40 = 0 _____(R: 5, -8)
24) x² + 5x + 6 = 0 _____(R:-2,-3)
25) x² - 7x + 12 = 0 _____(R:3,4)
26) x² + 5x + 4 = 0 _____(R:-1,-4)
27) 7x² + x + 2 = 0 _____(vazio)
28) x² - 18x + 45 = 0 _____(R:3,15)
29) -x² - x + 30 = 0 _____(R:-6,5)
30) x² - 6x + 9 = 0 _____(R:3)
31) ( x + 3)² = 1_______(R:-2,-4)
32) ( x - 5)² = 1_______(R:3,7)
33)( 2x - 4)² = 0_______(R:2)
34) ( x - 3)² = -2x²_______(R:vazio)

