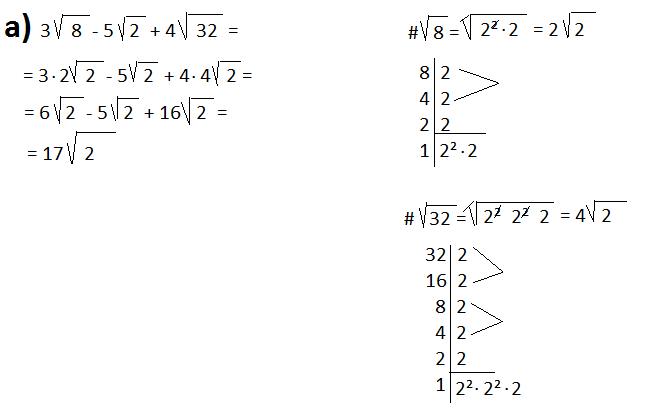“Divisão e Conquista: é uma técnica valiosa usada em momentos complicados, onde dividimos um grande problema em problemas menores até ser resolvido". Anatolii Karatsuba
domingo, 30 de agosto de 2015
Atividade matemática de culinária: Mousse de morango
Essa atividade tem como objetivo desmistificar as operações com números decimais.
Os alunos trouxeram os ingredientes e fizeram o mousse na sala de aula divididos em grupos.
Depois responderam as questões que seguem colando-as em seu caderno.
Receita do mousse de morango:
1 lata de leite condensado
1 lata de creme de leite
1 envelope de suco de morango
Morangos e chocolate granulado colorido para enfeitar.
Receita do mousse de morango:
1 lata de leite condensado
1 lata de creme de leite
1 envelope de suco de morango
Morangos e chocolate granulado colorido para enfeitar.
quinta-feira, 27 de agosto de 2015
Operações com radicais: exercícios e teoria com exemplos
RADICAIS SEMELHANTES
Radicais semelhantes são os que têm o mesmo índice e o mesmo radicando
Adição e subtração de radicais
1º Caso: Ocorre quando todos as raízes já se encontram com o mesmo radicando. Exs.:
2º Caso: Ocorre quando as raízes não são semelhantes, tendo assim, que serem todas reduzidas ao mesmo índice. Exs:
OBS: É importante saber, que, para resolver esse tipo de cálculo, a pessoa deve saber como reduzir raízes ao mesmo índice.
EXERCÍCIOS
1) Calcule
a) √9 + √4 =
b) √25 - √16 =
c) √49 + √16 =
d) √100 - √36 =
e) √4 - √1 =
f) √25 - ³√8 =
g) ³√27 + ⁴√16 =
h) ³√125 - ³√8 =
i) √25 - √4 + √16 =
j) √49 + √25 - ³√64 =
2) Efetue as adições e subtrações:
a) 2√7 + 3√7 =
b) 5√11 - 2√11 =
c) 8√3 - 10√3 =
d) ⁴√5 + 2⁴√5 =
e) 4³√5 - 6³√5 =
f) √7 + √7 =
g) √10 + √10 =
h) 9√5 + √5 =
i) 3.⁵√2 – 8.³√2 =
j) 8.³√7 – 13.³√7 =
k) 7√2 - 3√2 +2√2 =
l) 5√3 - 2√3 - 6√3 =
m) 9√5 - √5 + 2√5 =
n) 7√7 - 2√7 - 3√7 =
o) 8. ³√6 - ³√6 – 9. ³√6 =
p) ⁴√8 + ⁴√8 – 4. ⁴√8 =
3) Simplifique os radicais e efetue as operações:
a) √2 + √32=
b) √27 + √3 =
c) 3√5 + √20 =
d) 2√2 + √8 =
e) √27 + 5√3 =
f) 2√7 + √28 =
g) √50 - √98 =
h) √12 - 6√3 =
i) √20 - √45 =
4) Simplifique os radicais e efetue as operações:
a) √28 - 10√7 =
b) 9√2 + 3√50 =
c) 6√3 + √75 =
d) 2√50 + 6√2 =
e) √98 + 5√18 =
f) 3√98 - 2√50 =
g) 3√8 - 7√50 =
h) 2√32 - 5√18 =
5) Simplifique os radicais e efetue as operações:
a) √75 - 2√12 + √27 =
b) √12 - 9√3 + √75 =
c) √98 - √18 - 5√32 =
d) 5√180 + √245 - 17√5 =
MULTIPLICAÇÃO
a)1º Caso: Os radicais têm o mesmo índice. Efetuamos a operação entre os radicandos.
b)2º Caso: Os radicais não têm o mesmo índice. Inicialmente devemos reduzi-los ao mesmo índice.
Divisão
EXERCÍCIOS
6) Efetue as multiplicações e divisões:
a) √2 . √7 =
b) ³√5 . ³√10 =
c) ⁴√6 . ⁴√2 =
d) √15 . √2 =
e) ³√7 . ³√4 =
f) √15 : √3 =
g) ³√20 : ³√2 =
h) ⁴√15 : ⁴√5 =
i) √40 : √8 =
j) ³√30 : ³√10 =
7) Multiplique os radicais e simplifique o produto obtido:
a) √2 . √18 =
b) √32 . √2 =
c) ⁵√8 . ⁵√4 =
d) ³√49 . ³√7 =
e) ³√4 . ³√2 =
f) √3 . √12 =
g) √3 . √75 =
h) √2 . √3 . √6 =
8) Efetue as multiplicações e divisões:
a) 2√3 . 5√7 = (R: 10√21)
b) 3√7 . 2√5 = (R: 6√35)
c) 2. ³√3 . 3. ³√3 = (R: 6. ³√15)
d) 5.√3 . √7 = (R: 5√21)
e) 12. ⁴√25 : 2. ⁴√5 = (R: 6. ⁴√5)
f) 18. ³√14 : 6. ³√7 = (R: 3. ³√2)
g) 10.√8 : 2√2 = (R: 5√4)
Simplificação de radicais: exercícios , teoria e exemplos
Simplificar um radical significa escrevê-lo sob a forma mais simplis e equivalentes ao radical dado
1º) CASO: O índice e o expoente do radicando são divisíveis por um mesmo número (diferente de zero) Um radical não se altera quando o expoente do radicando e o índice do radical são divididos pelo mesmo número.
Exemplos
EXERCÍCIOS
1) Simplifique os radicais :
a) ⁴√5⁶ =
b) ⁸√7⁶ =
c) ⁶√3⁹ =
d) ¹⁰√8¹² =
e) ¹²√5⁹ =
f) ⁶√x¹⁰ =
g) ¹⁰√a⁶ =
h) ¹⁵√m¹⁰ =
i) ¹⁰√x⁵ =
j) ⁸√a⁴ =
2º CASO : O expoente do radical é um múltiplo do índice.
O radicando pode ser colocado Dora do radical com um expoente igual ao quociente do expoente anterior pelo índice.
Exemplos
a) √7¹⁰ = 7⁵ (Dividimos 10 por 2)
b) ³√7¹² = 7⁴ (Dividimos 12 por 3)
c) ⁴√7²⁰ = 7⁵ (Dividimos 20 por 4)
d) √a⁶ = a³ ( Dividimos 6 por 2)
EXERCÍCIOS
2) Simplifique os radicais:
a) √7⁸ =
b) ³√5⁹ =
c) ⁴√7¹² =
d) ⁵√9¹⁵ =
e) ³√3¹⁵ =
f) ⁴√6⁸ =
g) √9²⁰ =
h) √x² =
i) √x⁴ =
j) √a⁶ =
3º CASO: O expoente do radicando é maior do que o índice
Decompomos o radicando em fatores de modo que um dos fatores tenha expoente múltiplo do índice
EXERCÍCIOS
3) Simplifique os radicais
a) √a⁷ =
b) ³√m⁷ =
c) ⁴√m⁷ =
d) ⁵√x⁶ =
e) ⁷√a⁹ =
f) √7⁵ =
g) √2⁹ =
h) ³√5¹⁰ =
i) ⁴√7⁹ =
j) ⁵√6⁸ =
4) Fatore o radicando e simplifique os radicais:
a) √8 =
b) √27 =
c) ³√81 =
d) ⁴√32 =
e) √50 =
f) √80 =
g) √12 =
h) √18 =
i) √50 =
j) √8 =
k) √72 =
l) √75 =
m) √98 =
n) √99 =
o) √200 =
5) Calcule
a) √36 - √49 =
b) ³√8 + √64 =
c) -√100 - ³√64 =
d) -³√125 - ³√-1 =
e) ⁵√1 + √9 - ³√8 =
f) √100 +⁵√-32 + ⁶√0 =
g) ⁴√16 + ⁷√1 - ⁵√-1 =
Assinar:
Comentários (Atom)
Destaque!!!!!!!!!!!
Aula criativa de matemática sobre a conversão do dólar
Um emprego em um navio de cruzeiro pode ser uma grande chance de conhecer lugares novos e ganhar um bom salário. Quanto melhor for seu ingl...

-
O objeto capaz de medir o valor de um ângulo é chamado de transferidor, podendo ele ser de “meia volta” (180º) ou volta inteira (360º). ...
-
Frações: Própria, imprópria, aparente e números mistos. Temos que ter a noção básica de que toda fração é uma divisão. E que uma f...
-
A potenciação é uma multiplicação de fatores iguais Exemplos: 1) (1,2)² = 1,2 x 1,2 =1,44 2) (0,4)³ = 0,4 x 0,4 x 0,4 = 0,064 vamo...