Geometria espacial de posição

Primeiramente vamos diferenciar Postulados de Teoremas:

POSTULADOS- São verdades matemáticas que não precisam ser demostradas para aceitar-mos, já TEOREMAS-São verdades que precisam ser demostradas para que possamos aceita-la .

Postulados da  existência:

* Existem ponto, reta e plano.
* Numa reta , bem como fora dela, existem infinitos pontos.
* Numa reta existem pontos que pertencem a ela e outros que não pertencem.
* Num plano, bem como fora dele, existem infinitos pontos.
* Num ´plano existem pontos que pertencem ao plano e outros não.

Postulados da determinação:
*Dois pontos distintos determinam uma única reta.

*Três pontos não colineares determinam um único plano.

Postulado da inclusão:
Uma reta que possui dois pontos distintos em um plano está contida nesse plano.



Postulados das paralelas:por um ponto não pertencente a uma reta do espaço passa uma única reta paralela.










Posições relativas entre duas retas:
* Retas Concorrentes




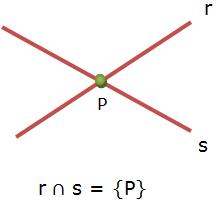
*Retas


*Retas Reversas ou não coplanares: duas retas que não te ponto em comum no plano.




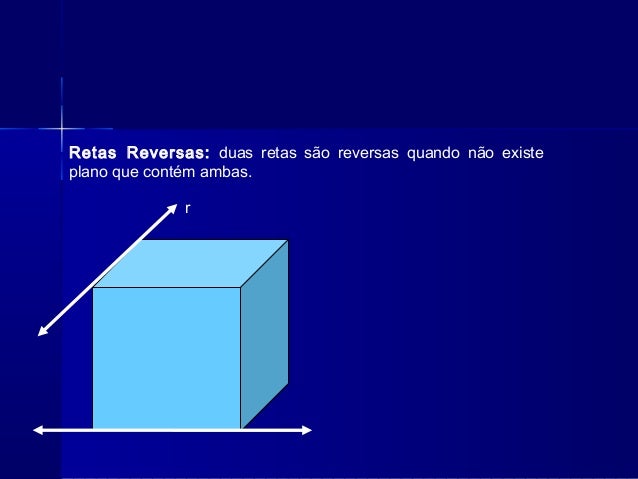
* Retas reversas ortogonais: retas quaisquer no espaço que formam ângulos retos.






* Retas perpendiculares: duas retas concorrentes que formam ângulos retos.




Determinação de plano: 

* Três pontos não colineares determinam um plano.
* Uma reta e um ponto fora dela determinam um plano.
* Duas retas paralelas distintas determinam um plano.
* Duas retas concorrentes determinam um plano.

Posições relativas entre uma reta e um plano
* Reta Contida: como já vimos, uma reta com dois de seus pontos em um plano está contida nesse plano.




* Reta secante ou concorrente: é uma reta que tem somente um único ponto em comum com o plano.





* Reta paralela ao plano: é uma reta que não tem nenhum ponto em comum com um plano.



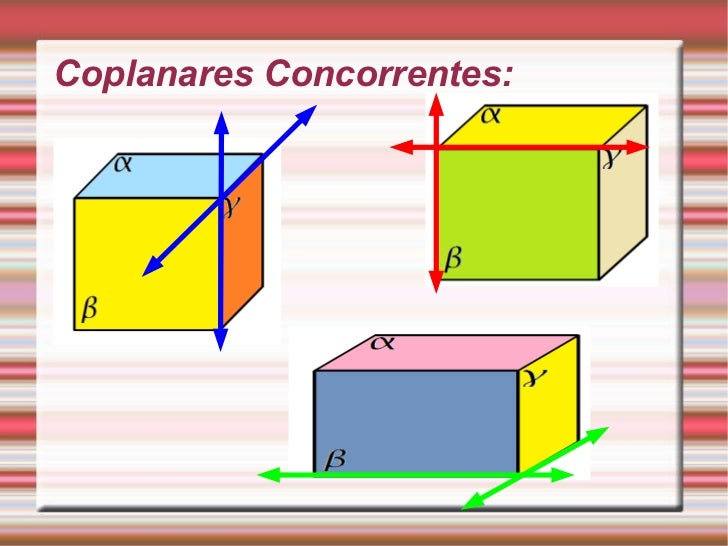
Posições relativas entre dois planos:
* Planos secantes ou concorrentes: dois planos distintos que tem um ponto em comum necessariamente tem uma reta em comum. 



Além do ponto P temos a reta r em comum. Assim a intersecção dos planos é a reta r.

* Planos paralelos:quando não existe nenhum ponto em comum entre os planos.



* Planos perpendiculares: quando um dos planos tem uma reta perpendicular ao outro.





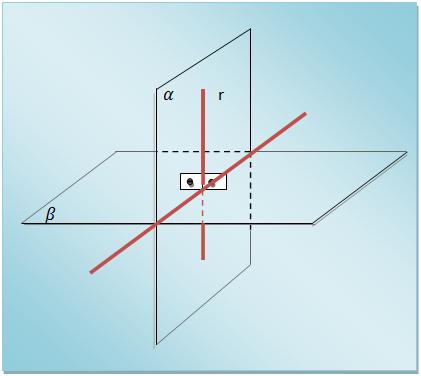
Projeção ortogonal

*Projeção ortogonal de um ponto sobre um ponto






*Projeção ortogonal paralela de um segmento de reta sobre um plano

*Projeção ortogonal não paralela de um segmento de reta sobre um plano

*Projeção ortogonal de uma reta sobre um plano

Pode ser oblíqua ou perpendicular como vemos na figura abaixo

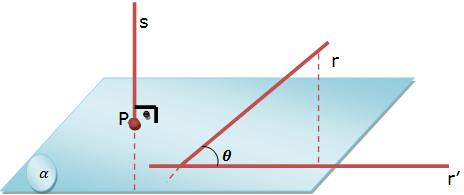
*Projeção ortogonal de uma reta paralela ao plano

Geometria espacial, sua aplicação no cotidiano e fórmulas

A Matemática teve seu surgimento a partir das necessidades fundamentais das pessoas, mais especificamente das necessidades econômicas . De uma maneira bastante similar , a geometria também surgiu. Geometria que significa: grego = geo =terra + metria= medida, ou seja, "medir terra", está ligada diretamente à necessidade de melhorar o sistema de recebimento de impostos de áreas rurais, e deve-se aos antigos egípcios que iniciaram o crescimento da disciplina.

Por sua vez a Geometria espacial funciona como uma prorrogação da Geometria plana, ela trabalha com o estudo da geometria no espaço (os objetos espaciais), como a relação entre esses elementos. Os objetos primários do modo de vista espacial, são: retas, pontos, segmentos de retas, curvas, planos, ângulos e superfícies. Os fundamentais tipos de cálculos que pode-se realizar são o de comprimentos de curvas, áreas de superfícies e volumes de regiões sólidas.

A Geometria Espacial corresponde a área da matemática que se encarrega de estudar as figuras no espaço, ou seja, aquelas que possuem mais de duas dimensões , tendo comprimento, largura e altura. Diferentemente da geometria plana que se ocupa de somente duas dimensões:comprimento e largura.

Contudo, o estudo das estruturas das figuras espaciais e suas inter-relações é determinado por alguns conceitos básicos como: Ponto, a reta e o  plano.

Vejamos um vídeo usando Minecraft sobre esse assunto:

Podemos representar o espaço por meio da projeção espacial das três dimensões, que são: altura, comprimento e largura. As coordenadas cartesianas são dadas pelos eixos x, y e z. Usando a localização de pontos, é possível traçar retas no espaço que formam planos e definem formas e estruturas geométricas.

Agora vamos perceber que a  geometria espacial sempre fez parte do nosso cotidiano: 

Nas caixas de chocolate ( Prisma de base triangular)

Na caixa de pizza com formato de um prisma octogonal .

Sabendo o conceito de Geometria espacial, conseguimos calcular quanto material precisamos para fazer "n" caixas de pintura de cabelo.

Nas caixas para guardar fotos

Nos livros

Nos materiais escolares

Embalagens de achocolatados

Favos de mel

Armários

Produtos de limpeza

Um dos exemplos da geometria Egípcia são as construções das pirâmides, e templos pelas civilizações egípcias e babilônias, sendo as provas mais antigas sobre o conhecimento de geometria. Porém, outros povos já utilizavam de teoremas como o de Pitágoras quadrado da hipotenusa de um triângulo retângulo.

Agora vejamos alguns exemplos de sólidos geométricos:

• Cubo

O cubo é um hexaedro regular composto de 6 faces quadrangulares, 12 arestas e 8 vértices sendo:

Área lateral: 4a2
Área total: 6a​2
Volume: a.a.a = a3

• Pirâmide 

A pirâmide é um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular, paralelogramo), um vértice (vértice da pirâmide) que une todas as faces laterais triangulares.

Sua altura corresponde a distância entre o vértice e sua base. 

Área total: Área lateral + área da base 

Volume: (Área da base. altura)/ 3

• Prisma

O Prisma é um poliedro composto de duas faces paralelas que formam a base, que por sua vez, podem ser triangular, quadrangular, pentagonal, hexagonal.

Além das faces o prima é composto de altura, lados, vértices e arestas unidos por paralelogramos. De acordo com sua inclinação, os prismas podem ser retos, aqueles em que a aresta e a base fazem um ângulo de 90º ou os oblíquos compostos de ângulos diferentes de 90º.

Área de cada Face: a.h
Área das Laterais: 6.a.h
Área da base: calculle a área de um triangulo do hexagono e faça vezes 6
Volume: Área da base. h

• Cone

• Cilindro

• Esfera

O ensino da geometria é de extrema importância para a vida cidadão no seu meio social, pois desenvolve o raciocínio visual , proporcionando ao aluno no seu desenvolvimento lógico e o crescimento da criatividade.