Triângulos: exercícios com gabarito e teoria

TRIÂNGULOS

Conceito: Triângulo é um polígono de três lados

Na figura acima:
= Os pontos A, B e C são vértices do triângulo.
= Os segmentos AB, BC e CA são os lados do triângulo.
= Os ângulos A, B e C são ângulos internos do triângulo

ÂNGULOS EXTERNO

Angulo externo é o ângulo suplementar do ângulo interno

PERÍMETRO

O perímetro de um  triângulo é igual à soma das medidas dos seus lados .

Perímetro ABC = AB + AC + BC



CLASSIFICAÇÃO DOS TRIÂNGULOS 


Quanto aos lados os trângulos se classificam em:

= Equilátero quando tem os três lados congruentes.
= Isósceles quando tem dois lados congruentes
= Escaleno quando não temlados congruentes

Quanto aos ângulos os triângulos se classificam em: 

= Acutângulo quando te três ângulos agudos 
= Retângulo quando tem um ângulo reto.
= Obtusângulo quando tem um angulo obtuso

Em um triângulo retângulo os lados que formam o ângulo reto chamam-se catetos e o lado oposto ao ângulo reto chama-se hipotenusa.

EXERCÍCIOS

1) Observe o triângulo retangulo e responda:

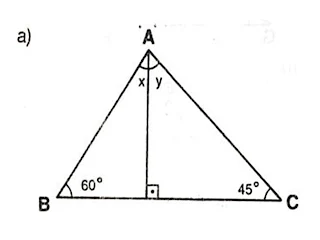
a) Quais são os vértices?
b) Quais são os lados?
c) Quais são os ângulos?

2) O perimetro de um triângulo é 25 cm. Dois lados medem respectivamente 7,8 cm e 8,2 cm.  Calcule a medida do terceiro lado?

3) Determine o comprimento do lado BC, sabendo que o perímewtro do triângulo ABC é 48 cm.

4) O perímetro do triângulo ´34 cm . Determine o comprimento do menor lado.

5) Classifique o triângulo de acordo com as medidas dos lados.

6) Classifique o triângulo de acordo com as medidas dos ângulos ;

7) Observe a figura e responda:

a) Que nome recebe o lado BC?

b) Que nome recebem os lados AB e AC?


ELEMENTOS NOTÁVEIS DE UM TRIÂNGULO

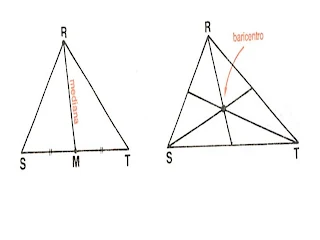
 Mediana de um triângulo é o segmento que une um vértice ao ponto médio do lado oposto.

Todo triângulo tem três medianas que se encontram em um ponto chamado baricentro

Bissetriz de um triângulo é o segmento da bissetriz de um ângulo interno que tem por extremidades o vértice desse ângulo e o ponto de encontro com o lado oposto.

Todo triângulo tem três bissetrizes que se encontram em um ponto interior chamado incentro.

Altura de um triângulo é o segmento de perpendicular traçada de um vértice ao lado oposto ou ao seu prolongamento

Todo o trângulo tem três alturas que se encontram em um ponto chamado ortocentro

SOMA DAS MEDIDAS DOS ANGULOS INTERNOS DE UM TRIÂNGULO

Observe os triângulos e as medidas dos ângulos internos

Vamos à demonstração desse teorema.

TEOREMA

Em qualquer triângulo, a soma das medidas dos ângulos internos é igual a 180° 

Prova

EXERCÍCIOS RESOLVIDOS

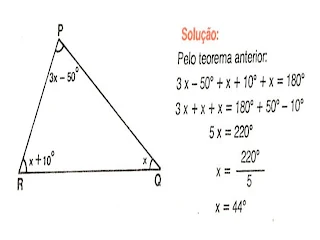
 Calcular x no triângulo abaixo:

Calcule x no triângulo abaixo:

 Calcule x no triângulo abaixo:

EXERCÍCIOS

8) Quanto vale a soma dos ângulos internos de um triângulo?

9) Copie e complete o quandro, sendo A,B e C ângulos internos de um triângulo.

10) Determine x em cada um dos triângulos

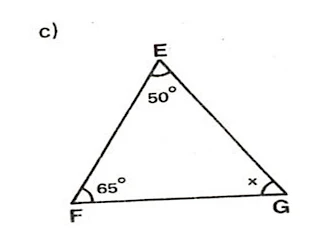
11) Determine x em cada um dos triângulos:

12) Determine a medida dos ângulos x, y e z.

TEOREMA DO ÂNGULO EXTERNO

Em qualquer triângulo, a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não-adjacentes.

Prova:

consideremos um triângulo ABC. vamos provar que m(ê) = m(Â) + m (B) 

Exemplos

Calcule o valor de x no triângulo abaixo:

EXERCÍCIOS

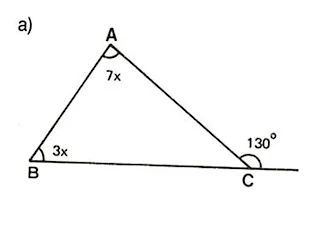
13) Determine a medida do ângulo externo indicado em cada triângulo:

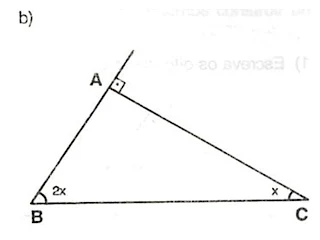
14) Calcule o valor de x nos triângulos dados:

15) Calcule o valor de x nos triângulos dados:

16) Calcule o valor de x nos triângulos dados:

17) Calcule o valor de x:

18) Calcule w e y :

CONCRÊNCIA DE TRIÂNGULOS

Intuitivamente, dois triângulos ABC e RST são congruentes se for possivel transportar um deles sobre o outro, de modo que eles coincidam.

Definição

Dois triângulos são chamados congruentes quando os lados e os angulos correspondentes são congruentes.

logo:

CASOS DE  CONGRUÊNCIA

O estudo dos casos de congruência de dois triângulos tem por finalidade estabelecer o menor número de condições para que dois triângulos sejam congruêntes.

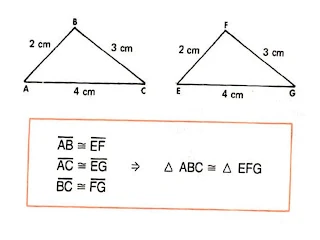
1º CAS0 : L. L. L. ( lado, lado, lado)

Dois triângulos que têm os três lados respectivamente congruentes são congruentes.

2º CASO L. A. L. (lado, ângulo,  lado)

Dois treângulos que têm dois lados e o ângulo por eles formados respectivamente congruentes são con gruentes.

3º CASO A. L. A. ( ângulo, lado , ângulo)

Dois triângulos que tem um lado e dois ângulos adjacentes a esse lado respectivamente congruentes são congruentes.

4º CASO : L. A. A° ( lado , ângulo, ângulo oposto)

Dois trângulos que têm um lado, um ângulo adjacente e um ângulo oposto a esse lado respectivamente congruentes são congruentes.

EXERCÍCIOS

19) Cite, em cada item, o caso de congruência dos triângulos.