Minecraft na geometria de posição

A matemática no desenho técnico: perspectiva, principais vistas em exemplos e exercícios

Quem trabalha com desenho técnico sabe o quanto é importante interpretá-los corretamente usando a matemática, executar representação, ler e interpretar os desenhos em diversas perspectivas e projeções. Essa parte da matemática também é muito utilizado na arquitetura, urbanismo e projetista de peças.






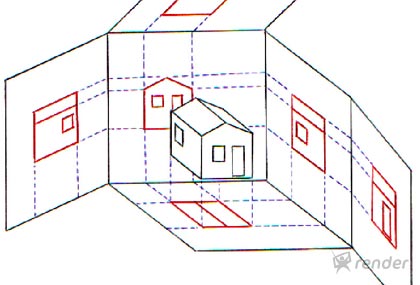
Quando falamos sobre a representação de um objeto que pode ser observado por meio de diferentes vistas.

Vista é a projeção paralela ortogonal através do plano de projeção onde representamos detalhes do objeto de acordo com o lado que está sendo observado. O ponto de partida é determinar qual lado será considerado frente. As principais vistas são:

* frontal: é a vista principal da peça, determina as posições das demais vistas;

*superior

* lateral esquerda

* lateral direita

Na prática, porém as projeções são representadas como na figura abaixo, onde os planos de projeção são rebatidos sobre um mesmo plano.

Quando desenhamos vistas sobre um mesmo plano, eliminamos o desenho dos planos, deixando apenas as linhas que separam os desenhos das vistas.

Uso das Projeções Ortogonais

A aplicação das projeções ortogonais na representação das superfícies que compõem, respectivamente, um cilindro, um paralelepípedo e um prisma de base triangular. As superfícies projetadas no plano vertical estão em vista frontal (V.F.) do técnico em mecânica.

Para que apareça essa terceira dimensão, é necessário fazer uma segunda projeção ortogonal, em que as superfícies projetadas no plano horizontal são obtidas na vista superior (V.S.) do técnico em mecânica (Figura 5).

Ao analisar um dado objeto para projeção nos três planos, formar-se-ão as projeções ortogonais para cada plano 

O rebatimento dos planos de projeção do objeto nas três vistas obtidas em cada plano.

Dependendo do grau de complexidade do objeto, as vistas principais não são suficientes para representar todos os detalhes. Nesse caso, podemos usar até seis vistas.

Exercícios:

1) Nos desenhos a seguir, faça a identificação dos planos que compõem as formas espaciais das peças dadas e analise seus rebatimentos nas vistas correspondentes.

2) Faça as projeções ortogonais em 1º e 3º diedros para os desenhos das peças a seguir.

3) Faça a identificação dos planos que compõem a peça abaixo:

Distancias: de um ponto a uma reta, de um ponto a um plano, entre duas retas, entre uma reta e um plano, entre planos, entre retas reversas

1)  Distância de um ponto a uma reta

A distância entre uma reta e um plano é a distância entre um ponto qualquer da reta e o plano e será obtida traçando uma perpendicular a reta r, sendo o ponto P a intersecção. Indicamos por d (P, r) = d (P, P')

2)  Distância de uma reta e um plano A distância entre uma reta e um plano paralelo é a distância entre um ponto qualquer da reta e o plano, sendo o ponto P perpendicular a reta r: 3)  Distância entre duas retas paralelas A distância entre duas retas paralelas é a distância de um ponto qualquer de uma delas à outra. 4)  Distância entre uma reta em plano paralelo A distância entre uma reta e um plano à ela é a distância de um ponto perpendicular qualquer da reta ao plano. 5)  Distância entre dois planos paralelos A distância entre dois planos paralelos é a distância entre um ponto perpendicular qualquer de um deles e o outro plano: 6)  Distância entre duas retas reversas É a distância do menor segmento com extremidades que formam 90º. Podemos perceber que a distância entre as retas r e s s é a medida do segmento AB. Obs: Quando as  forem concorrentes entre si, a distância entre elas é zero, como na segunda figura. Reforçando o conceito: a distância entre retas retas reversas é o segmento que forma com suas extremidades uma perpendicular. Na figura abaixo t á perpendicular com entre as retas reversas r e s e o comprimento do segmento PQ é a distância entre elas.

Exercícios geometria espacial de posição

1) Se r é uma reta oblíqua ao plano P, quantos são os planos que contêm r e são perpendiculares a P?

A)	0
B)	1
C)	2
D)	4
E)	Infinitos

2) Considerando a figura abaixo, onde a reta r é perpendicular ao plano a e s é uma reta desse mesmo plano, assinale o que for correto:

1-	r e s são perpendiculares.
2-	r e s determinam um plano perpendicular a a.
4-	O triângulo PMN é equilátero.
8-	r pertence a α.
16-	A soma dos ângulos q1 e q2 é 90o.

3) Na cadeira representada na figura abaixo, o encosto é perpendicular ao assento e este é paralelo ao chão.

Sendo assim,

A)	Os planos EFN e FGJ são paralelos.
B)	HG é um segmento de reta comum aos planos EFN e EFH.
C)	Os planos HIJ e EGN são paralelos.
D)	EF é um segmento de reta comum aos planos EFN e EHG.

4) Sobre a posição relativa de planos no espaço, é correto afirmar:

A)	Se os planos α e β são perpendiculares a um plano λ, então α é paralelo a β.
B)	Se dois planos, α e β, são paralelos entre si, então a interseção de qualquer outro plano λ com estes é um par de retas paralelas.
C)	Por uma reta r perpendicular a um plano passam apenas dois planos, β e λ, perpendiculares ao plano α.
D)	Por um ponto P não pertencente a um plano α passam infinitos planos paralelos ao plano α.
E)	Dois planos, α e β, paralelos a uma mesma reta r são paralelos entre si.

5) Sejam a e b dois planos paralelos e seja r uma reta de a. Assinale a sentença verdadeira:

A)	Toda reta de b é paralela a r.
B)	Toda reta perpendicular a b é perpendicular a r.
C)	Não existe em b uma reta paralela a r.
D)	Se s é uma reta de b, não paralela a r, existem em b uma reta concorrente com s e paralela a r.
E)	Se s é uma reta de b, não paralela a r, existe em b uma reta paralela a s, que é paralela a r.

6) Considere um plano a e um ponto P qualquer do espaço. Se por P traçarmos a reta perpendicular a a , a intersecção dessa reta com a é um ponto chamado projeção ortogonal do ponto P sobre a . No caso de uma figura F do espaço, a projeção ortogonal de F sobre a é definida pelo conjunto das projeções ortogonais de seus pontos. Com relação a um plano a qualquer fixado, pode-se dizer que:

A)	a projeção ortogonal de um segmento de reta pode resultar numa semi-reta;
B)	a projeção ortogonal de uma reta sempre resulta numa reta;
C)	a projeção ortogonal de uma parábola pode resultar num segmento de reta.
D)	a projeção ortogonal de um triângulo pode resultar num quadrilátero;
E)	a projeção ortogonal de uma circunferência pode resultar num segmento de reta.

7) Sobre retas e planos no espaço, verifica-se:

1-	Se uma reta r é paralela a um plano a, qualquer plano que contém r é paralelo a a.
2-	Dois planos paralelos a uma reta r podem ser paralelos entre si.
4-	Duas retas no espaço são sempre concorrentes ou paralelas ou coincidentes.
8-	Uma reta ortogonal a duas retas de um plano é perpendicular a esse plano.
16-	Por uma reta perpendicular a um plano a passa uma infinidade de planos perpendiculares a a.
32-	Três pontos não alinhados determinam um plano.

8) Leia as afirmativas abaixo e escolha a alternativa correta:

I. Dados um plano a e dois pontos A e B fora dele é sempre possível passar por A e B um plano perpendicular a a  .

II. Dadas 2 retas reversas a e b não existe nenhum plano eqüidistante das duas retas.

III. Se a intersecção de duas retas é o conjunto vazio, elas são paralelas ou reversas.

IV. Quatro pontos distintos e não-coplanares determinam exatamente 5 planos.

V. Se dois planos forem perpendiculares, todo plano perpendicular a um deles será perpendicular ao outro.

São verdadeiras:

A)	apenas uma afirmação.
B)	apenas duas afirmações.
C)	apenas três afirmações.
D)	apenas quatro afirmações.
E)	todas são falsas. 9) Classifique em Verdadeiro (V) ou Falso (F) cada afirmação a seguir: 1) (       ) Duas retas que têm um ponto comum são concorrentes. 2) (       ) Se dois planos têm uma reta comum, eles são secantes. 3) (       ) Se dois planos têm uma única reta comum, eles são secantes. 4) (       ) Uma reta e um plano que têm um ponto comum são concorrentes. 5) (       ) Quando uma reta está contida num plano, eles têm um ponto em comum. 6) (       ) Se uma reta é paralela a um plano, ela é paralela a qualquer reta do plano. 7) (       ) Se um plano é paralelo a uma reta, qualquer reta do plano é reversa a reta dada. 8) (       ) Se uma reta é paralela a um plano, ela é paralela a infinitas retas do plano. 9) (       ) Se duas retas distintas são paralelas a um plano, então elas são paralelas entre si. 10) (     ) Dadas duas retas reversas, sempre existe uma reta que se apóie em ambas. 11) (     ) Se dois planos são secantes, então uma reta de um deles pode ser reversa com uma reta do outro. 12) (     ) Dois planos distintos paralelos têm um ponto comum. 13) (     ) Se dois planos distintos são paralelos, então uma reta de um deles é paralela ao outro. 14) (     ) Se dois planos distintos são paralelos, uma reta de um e uma reta do outro são reversas ou paralelas. 15) (     ) Se uma reta é paralela a dois planos, então esses planos são paralelos. 16) (     ) Se dois planos são paralelos a uma reta, então são paralelos entre si. 17) (     ) Se um plano contém duas retas paralelas a um outro plano, então estes planos são paralelos. 18) (     ) Se duas retas de um plano são, respectivamente, paralelas a duas retas concorrentes do outro plano, então estes planos são paralelos. 19) (     ) Uma reta perpendicular a um plano é perpendicular a todas as retas do plano. 20) (     ) Uma reta perpendicular a um plano forma ângulo reto com qualquer reta do plano. 21) (     ) Se uma reta é ortogonal a duas retas distintas de um plano, então ela é perpendicular ao plano. 22) (     ) Dadas duas retas distintas de um plano, se uma outra reta é perpendicular a primeira e ortogonal a segunda, então ela é perpendicular ao plano. 23) (     ) Duas retas reversas são paralelas a um plano. Toda reta ortogonal a ambas é perpendicular ao plano. 24) (     ) Uma reta e um plano são paralelos. Toda reta perpendicular a reta dada é perpendicular ao plano. 25) (     ) Se dois planos são perpendiculares, então toda reta de um deles é perpendicular ao outro. 26) (     ) Se uma reta é perpendicular a um plano, por ela passa um único plano, perpendicular ao plano dado. 27) (     ) Dois planos perpendiculares a um terceiro são perpendiculares entre si. 28) (     ) Se dois planos são perpendiculares a um terceiro, então eles são paralelos. 29) (     ) Se dois planos são perpendiculares, então toda reta perpendicular a um deles é paralela ao outro ou está contida neste outro. 30) (     ) Se dois planos são paralelos, todo plano perpendicular a um deles, é perpendicular ao outro. Gabarito: 1 – F 2 – F 3 – V 4 – F 5 – V 6 – F 7 – F 8 – V 9 – F 10 – V 11 – V 12 – F 13 – V 14 – V 15 – F 16 – F 17 – F 18 – V 19 – F 20 – V 21 – F 22 – F 23 – V 24 – F 25 – F 26 – F 27 – F 28 – F 29 – V 30 – V     10) Quais são as maneiras de se determinar um plano? 11) Dê a definição de: a) Retas paralelas. b) Retas concorrentes. c) Retas reversas. d) Planos secantes. e) Planos paralelos distintos. f) Planos paralelos coincidentes. 12) Descreva e desenhe duas situações onde uma reta é perpendicular a um plano. 13) Justifique se as afirmações abaixo são falsas (F) ou verdadeiras (V): a) Dois planos distintos que têm uma reta comum são secantes. b) Dois planos secantes têm infinitos pontos comuns. c) Se dois planos distintos são paralelos, qualquer reta de um deles é paralela a qualquer reta do outro. d) Se dois planos distintos são paralelos, qualquer reta de um deles é paralela ao outro. e) Se duas retas são paralelas um plano a, elas pertencem ao mesmo semi-espaço determinado por a. f) Para que, em relação a a, dois planos pertençam ao mesmo semi-espaço, é necessário que os três planos sejam paralelos. Resolução: a) Dois planos distintos que têm uma reta comum são secantes. V Se os planos fossem paralelos, não teriam reta comum a eles. Para que uma reta seja tanto de um plano quanto do outro, os planos devem se interceptar, ou seja, devem ser secantes. b) Dois planos secantes têm infinitos pontos comuns. V Se dois planos são secantes, eles se encontram.  No encontro desses planos forma uma reta e essa reta tem infinitos pontos, porque o plano é infinito. c) Se dois planos distintos são paralelos, qualquer reta de um deles é paralela a qualquer reta do outro. F Imagine duas folhas (uma sobre a outra). Faça um desenho de uma reta numa folha e um desenho de reta na outra folha. Essas retas podem ser paralelas, mas nem todas serão. Podemos desenhar uma reta horizontal numa e vertical na outra. Não serão paralelas. d) Se dois planos distintos são paralelos, qualquer reta de um deles é paralela ao outro. V Uma reta num plano será paralela ao outro plano,qualquer que seja a posição dela. e) Se duas retas são paralelas um plano a, elas pertencem ao mesmo semi-espaço determinado por a. F Imagine uma folha de papel. Coloque uma reta em cima e outra embaixo de forma que as duas fiquem paralelas ao plano. Uma está num semi-espaço e a outra está no outro semi-espaço. f) Para que, em relação a a, dois planos pertençam ao mesmo semi-espaço, é necessário que os três planos sejam paralelos. V Imagine uma folha. Deixe-a sobre a mesa. Da mesa para cima temos um semi-espaço. Para que duas outras folhas estejam sempre acima da mesa, elas devem estar paralelas a primeira folha. Caso uma delas não fosse paralela, em  algum momento essa folha ao ser esticada (pois o plano é infinito), ela iria tocar na mesa e iria "vazar" para o outro semi-espaço.  14) Responda V ou F:  a)  Três pontos distintos determinam um único plano. b)   Os vértices de um triângulo são coplanares. c)   Se três pontos são coplanares, então el es são colineares. Respostas e justificativas: a)  Falsa. Três pontos distintos podem estar numa mesma reta e nesse caso eles não determinam um único plano. [Fig. 1]. Os três pontos precisariam não ser colineares para que ficasse determinado um único plano [Fig. 2]. b) Verdadeira. Os vértices de um triângulo são três pontos não colineares. Eles determinam um plano que contém o triângulo [Fig. 2]. c)   Falsa. Três pontos podem ser coplanares sem estarem na mesma reta [Fig. 2]. 15) Quantos são os planos determinados por três retas, duas a duas concorrentes, todas passando num mesmo ponto. Resposta: Sendo a,b e c as retas, há duas possibilidades: ou as retas estão num mesmo plano α [ Fig. 1 ] ou os planos α = (b,c) , β = (a,c) e γ = (a,b) estão determinados [ Fig. 2 ] .  Logo, as três retas determinam um ou três planos. 16) Classifique cada sentença como verdadeira ou falsa: a)                 Dado um ponto, existe uma única reta passando por ele. b)                 Dado um ponto, existe uma reta passando por ele. c)                 Dado um ponto, existem infinitas retas que o contêm. d)                 Dados dois pontos distintos, existe um plano que os contém. e)                 Três pontos não alinhados determinam três retas. f)                   Três pontos não alinhados determinam um plano. g)                 Três retas determinam um plano. h)                 Um ponto e uma reta que não o contém determinam um plano. 17) Quatro pontos, A, B, C, D não são coplanares. Quantos planos eles determinam? Quais são? 18) É comum encontrarmos mesas com quatro pernas que, mesmo apoiadas em um piso plano, balançam, obrigando a colocação de um calço em uma das pernas. Com base no que você estudou até aqui, explique por que isso acontece. 19) Quantos planos são determinados por três retas distintas, duas a duas concorrentes e que não passam por um mesmo ponto? 20) Quantos são os planos determinados por três retas distintas, duas a duas paralelas? (http://www.matematiques.com.br)