Exercícios sobre ângulos opostos pelo vértice

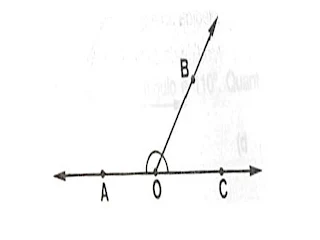
Duas retas concorrentes determinam quatro ângulos, dois a dois , opostos pelo vértice

Na figura:

â e  c são opostos pelo vértice.

m e n são opostos pelo vértice

TEOREMA

Dois ângulos opostos´pelo vértice são congruentes.

prova:

Sejam os ângulos a e b opostos pelo vértice.

1) m(â) + m(^c) = 180°

2) m(b) + m(c) = 180°

comparando : m(â) + m(c) = m(b) + m(c)

m(â) = m(b)

Se a e b têm a mesma medida, eles são congruentes.

EXECÍCIOS

1) Quais são os 3 pares de ângulos opostos pelo vértice?

2)  Se x = 50° , determine y, m e n:

3) Calcule os ângulos x,y, z e w da figura:

4) Calcule os ângulos x, y e z das figuras:

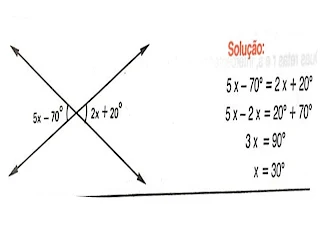
5) Calcule x:

6) Calcule x:

7) Calcule x :

8) Calcule x:

9) As medidas de dois ângulos opostos pelo vértice são expressas em graus por  15x - 14° e 3x + 10°. Quanto vale x?

10) As medidas de dois ângulos opostos pelo vértice são expressas em graus por (2m - 50) e (m + 35). Quanto vale m?

Exercícios sobre ângulos suplementares somam 180º

Dois ângulos são suplementares quando a soma de suas medidas é 180°

m(AÔB) + m(BÔC) = 180°

Exemplos:

= 50° e 130° são angulos suplementares, porque 50° + 130° = 180°

= 125° e 55° são ângulos suplementares, porque 125°  + 55º = 180°

EXERCÍCIOS

1) Responda:

a) Um ângulo de 70° e um de 110° são suplementares?
R: (

b) Um ângulo de 155° e um de 25° são suplementares?

2) Calcule o suplemento dos seguintes ângulos:
a) 30° = (R:
b) 85° = (R: 
c) 72° = (R: 
d) 132° 30´ = (R: 
e) 140° 20´ = (R: 
f) 151° 40` =(R:


3) Determine x, sabendo que os ángulos são suplementares:

4) Determine x, sabendo que os ângulos são suplementares:



5) Calcule x:

6) A quarta parte da medida de um ângulo mede 30°. Calcule a medida do seu suplemento.

7) A medida de um ângulo é igual à medida de seu suplemento. Calcule esse ângulo.

8) Calcule a medida de um ângulo que é igual ao triplo de seu suplemento.

9) O dobro da medida de um ângulo é igual à medida do suplemento desse ângulo. Calcule a medida do ângulo.

10) O triplo da medida de um ângulo mais a medida do suplemento desse ângulo é 250°. Calculo a medida do ângulo.

11) Calcule a medida de um ângulo cuja medida é igual a 2/3 do seu suplemento.

12) A soma do complemento com o suplemento de um ângulo é 110° . Quanto mede o ângulo?

Exercícios sobre ângulos complementares somam 90°

ÂNGULOS COMPLEMENTARES

Dois angulos são complementares quando am soma de suas medidas é 90°

m(AÔB) + m((BÔC) = m(AÔC)

Exemplos:

 65° e 25° são ângulos complementares , porque 65° + 25° = 90°

EXERCÍCIOS 

1) Responda: 

a) Um ângulo de 20° e um de 70° são complementares?
b) Um ângulo de 35° e um de 65° são complementares?
c) Um ângulo de 73° e um de 27° são complementares?
d) Um ângulo de 58° e um de 32° são complementares?


2) Calcule o complemento dos seguintes ângulos:

a) 34°
b) 72°
c) 84°
d) 18° 25´
e) 40° 30´
f) 51° 20´

3) Resolva as equações abaixo, onde a inc´gnita x é um ângulo (medido em graus)

a) 2x = 90°
b) x + 17° = 90°
c)  4x + 10° = 90°
d) x + 8x = 90°
e) 5x - 20° = 1° = 2x
f) x = 2( 90° - x)
g) 4( x + 3° 0 = 20°
h) ( 3x - 20° ) + 50° = 90°
I) 3( x + 1°) = 2( x  + 7°)
J) 2x + 2 (x + 1° ) = 4° + 3 ( x + 2°)

4) Determine x, sabendo que os ângulos são complementares:

5) Dado um ângulo de medida x, indicar:

a) o seu complemento.

b) o dobro do seu complemento

c) o triplo do seu complemento.

d) a metade do seu complemento

e) a terça parte do seu complemento

7) A medida de um ângulo é igual à medida de seu comprimento, quanto mede esse  ângulo?

8) A medida de um ângulo é a metade da medida do seu comprimento. Calcule a medida desse ângulo.

9) Calcule a medida de um ângulo cuja medida é igual ao triplo de seu complemento.

10) A diferença entreo o dobro da medida de um ângulo e o seu complemnto é 45° Calcule a medida desse ângulo.

11) A terça parte do complemento de um ângulo mede 20°. Qual a medida do ângulo?

12) Dois ângulos complementares têm suas medidas expressas em graus por 3x + 25° e 4x - 5° . Quanto medem esses ângulos?

Exercícios de potenciação com expoente negativo

O sinal negativo de um expoente não passa de um código que está nos alertando que a base está invertida. Com essa nova interpretação, a regra do expoente negativo se transforma em uma regra simples e fácil de ser aplicada no jogo matemático. Mas não esqueça: foi uma propriedade que a gerou.
Nos casos em que o expoente é negativo, devemos trocar o sinal do expoente e inverter a base racional, isto é, o numerador passa a ser denominador e o denominador passa a ser numerador. Observe os exemplos:

EXERCÍCIOS

1) Calcule as potências:

a) 4⁻² = 
b) 4⁻³ = 
c) 5⁻¹ = 
d) 3⁻³ = 
e) 10⁻² = 
f) 10⁻³ = 
g) 2⁻⁵ = 
h) 7⁻¹ = 
i) 1⁻¹⁸ = 

2) Calcular as potências

a) (-5)⁻² = 
b) (-3)⁻⁴ = 
c) (-2)⁻⁵ = 
d) (-5)⁻³ = 
e) (-1)⁻⁴ = 
f) (-1)⁻⁵ =


3) Calcule as potências

a) (3/7)⁻² = 
b) (2/5)⁻¹ =
c) (1/3)⁻³ = 
d) (-5/4)⁻³ =
e) (-1/3)⁻² = 
f) (-2/5)⁻³ =
4) Resolva as potências:
a)      ( -4 )^-2 =

b)      ( + 3) ³ =

c)      ( - ²/₇) ² =

^d)        ( + ¾  )^-4 =

e)      ( + ¹/₅) ⁵=

f)      ( - ¹²/₁₃) ¹ =
g)      ( + ⁵/₉) ^-2 =

h)      ( + ²/₇) ⁴ =

i)      ( - ²/₃) ⁵ =

j)      ( - ³/₅) ^-3=
5) O número de elementos distintos da sequência 2⁴, 4², 4^-2 (-4)², (-2)⁴, (-2)^-4 é:

a) 1
b) 2
c) 3
d) 4

6) O valor da expressão B = 5 . 10⁸ . 4 . 10^-3 é:

a) 20⁶
b) 2 . 10⁶
c) 2 . 10⁹
d) 20 . 10^-4

7) O valor da expressão C = (10^-3 x 10⁵) / (10 x 10⁴) é:

a) 10
b) 1000
c) 10^-2
d) 10^-3

8) Quais os resultados de 7¹³ : 7¹¹ e de 2^-4 _. 2⁵ ?

9)  Reduza a uma única potência e calcule o seu valor:
a) 10² . 10^-4 =
b) 2³ . 2⁶ =
c) 3⁸ . 3^-5 =
d) 3⁴ : 3 =
e) 2⁸ : 2⁴ =
f ) 2⁶ : 2⁹ =

10) Calcule a expressão (1/2)^-3 + (1/2)^-5 :

11)Calcule:

a) 7⁻² = 
b) 5⁻³ = 
c) 2⁻⁴ = 
d) 2⁻⁵ = 
e) (-3)⁻² = 
f) –(-3)⁻² = 

12)Calcule:

a) (3/2)⁻² = 
b) (1/2)⁻³ = 
c) (2/3)⁻² = 
d) (-1/4)⁻² = 
e) (5/2)⁻³ = 
f) (-1/2)⁻⁴ = 

13) Calcule:

a) (-4)² - 3 = 
b) 1 + (-2)³ = 
c) -2 + (-5)² = 
d) 15 + (-1)⁷ -2 =
e) (-2)² + (-3)³ +1 = 
f) (-9)² -2 –(-3) -6 = 
g) (-2) . (-7) + (-3)² = 
h) (-1)³ + 3 + (-2) . (-5) =

14) Calcule o valor das expressões:

a) (-4/3)² - 1 = 
b) 3/2 + (-1/2)² -8 = 
a) (1 - ½)² + (-1 + ½)³ = 
b) (1 + ½)² - ¼ = 

• 
  
• 
  

(Material de referência jmpmat13.blogspot.com)