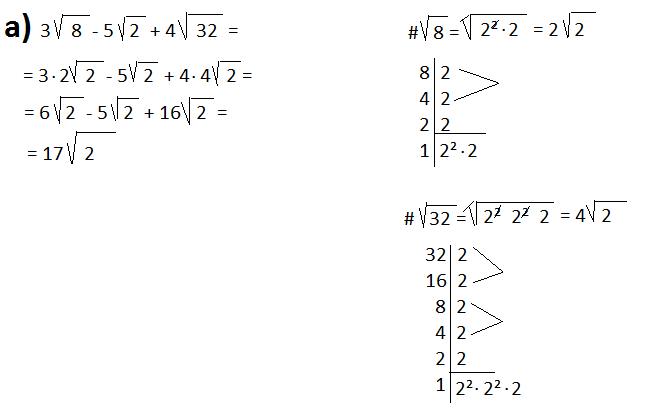Operações com radicais: exercícios e teoria com exemplos

RADICAIS SEMELHANTES
Radicais semelhantes são os que têm o mesmo índice e o mesmo radicando

Adição e subtração de radicais

1º Caso: Ocorre quando todos as raízes já se encontram com o mesmo radicando. Exs.:

2º Caso: Ocorre quando as raízes não são semelhantes, tendo assim, que serem todas reduzidas ao mesmo índice. Exs:

OBS: É importante saber, que, para resolver esse tipo de cálculo, a pessoa deve saber como reduzir raízes ao mesmo índice.

EXERCÍCIOS

1) Calcule

a) √9 + √4 = 
b) √25 - √16 = 
c) √49 + √16 = 
d) √100 - √36 = 
e) √4 - √1 = 
f) √25 - ³√8 = 
g) ³√27 + ⁴√16 = 
h) ³√125 - ³√8 = 
i) √25 - √4 + √16 = 
j) √49 + √25 - ³√64 = 



2) Efetue as adições e subtrações:

a) 2√7 + 3√7 = 
b) 5√11 - 2√11 = 
c) 8√3 - 10√3 = 
d) ⁴√5 + 2⁴√5 = 
e) 4³√5 - 6³√5 = 
f) √7 + √7 = 
g) √10 + √10 = 
h) 9√5 + √5 = 
i) 3.⁵√2 – 8.³√2 = 
j) 8.³√7 – 13.³√7 = 
k) 7√2 - 3√2 +2√2 = 
l) 5√3 - 2√3 - 6√3 = 
m) 9√5 - √5 + 2√5 = 
n) 7√7 - 2√7 - 3√7 = 
o) 8. ³√6 - ³√6 – 9. ³√6 = 
p) ⁴√8 + ⁴√8 – 4. ⁴√8 = 

3) Simplifique os radicais e efetue as operações:

a) √2 + √32= 
b) √27 + √3 = 
c) 3√5 + √20 =
d) 2√2 + √8 = 
e) √27 + 5√3 = 
f) 2√7 + √28 = 
g) √50 - √98 = 
h) √12 - 6√3 =
i) √20 - √45 = 

4) Simplifique os radicais e efetue as operações:

a) √28 - 10√7 = 
b) 9√2 + 3√50 = 
c) 6√3 + √75 = 
d) 2√50 + 6√2 = 
e) √98 + 5√18 = 
f) 3√98 - 2√50 = 
g) 3√8 - 7√50 = 
h) 2√32 - 5√18 = 

5) Simplifique os radicais e efetue as operações:

a) √75 - 2√12 + √27 = 
b) √12 - 9√3 + √75 = 
c) √98 - √18 - 5√32 = 
d) 5√180 + √245 - 17√5 = 



MULTIPLICAÇÃO 

a)1º Caso: Os radicais têm o mesmo índice. Efetuamos a operação entre os radicandos.

b)2º Caso: Os radicais não têm o mesmo índice. Inicialmente devemos reduzi-los ao mesmo índice.



Divisão


EXERCÍCIOS

6) Efetue as multiplicações e divisões:

a) √2 . √7 =
b) ³√5 . ³√10 =
c) ⁴√6 . ⁴√2 =
d) √15 . √2 = 
e) ³√7 . ³√4 =
f) √15 : √3 = 
g) ³√20 : ³√2 = 
h) ⁴√15 : ⁴√5 = 
i) √40 : √8 = 
j) ³√30 : ³√10 = 

7) Multiplique os radicais e simplifique o produto obtido:

a) √2 . √18 = 
b) √32 . √2 = 
c) ⁵√8 . ⁵√4 = 
d) ³√49 . ³√7 = 
e) ³√4 . ³√2 = 
f) √3 . √12 = 
g) √3 . √75 = 
h) √2 . √3 . √6 = 

8) Efetue as multiplicações e divisões:

a) 2√3 . 5√7 = (R: 10√21)
b) 3√7 . 2√5 = (R: 6√35)
c) 2. ³√3 . 3. ³√3 = (R: 6. ³√15)
d) 5.√3 . √7 = (R: 5√21)
e) 12. ⁴√25 : 2. ⁴√5 = (R: 6. ⁴√5)
f) 18. ³√14 : 6. ³√7 = (R: 3. ³√2)
g) 10.√8 : 2√2 = (R: 5√4)

Simplificação de radicais: exercícios , teoria e exemplos

Simplificar um radical significa escrevê-lo sob a forma mais simplis e equivalentes ao radical dado

1º) CASO: O índice e o expoente do radicando são divisíveis por um mesmo número (diferente de zero) Um radical não se altera quando o expoente do radicando e o índice do radical são divididos pelo mesmo número.

Exemplos



EXERCÍCIOS

1) Simplifique os radicais :

a) ⁴√5⁶ = 
b) ⁸√7⁶ = 
c) ⁶√3⁹ = 
d) ¹⁰√8¹² = 
e) ¹²√5⁹ = 
f) ⁶√x¹⁰ = 
g) ¹⁰√a⁶ = 
h) ¹⁵√m¹⁰ = 
i) ¹⁰√x⁵ = 
j) ⁸√a⁴ = 

2º CASO : O expoente do radical é um múltiplo do índice.

O radicando pode ser colocado Dora do radical com um expoente igual ao quociente do expoente anterior pelo índice.

Exemplos

a) √7¹⁰ = 7⁵ (Dividimos 10 por 2)
b) ³√7¹² = 7⁴ (Dividimos 12 por 3)
c) ⁴√7²⁰ = 7⁵ (Dividimos 20 por 4)
d) √a⁶ = a³ ( Dividimos 6 por 2)

EXERCÍCIOS

2) Simplifique os radicais:

a) √7⁸ = 
b) ³√5⁹ = 
c) ⁴√7¹² = 
d) ⁵√9¹⁵ = 
e) ³√3¹⁵ = 
f) ⁴√6⁸ = 
g) √9²⁰ = 
h) √x² = 
i) √x⁴ = 
j) √a⁶ = 

3º CASO: O expoente do radicando é maior do que o índice

Decompomos o radicando em fatores de modo que um dos fatores tenha expoente múltiplo do índice




EXERCÍCIOS

3) Simplifique os radicais

a) √a⁷ = 
b) ³√m⁷ = 
c) ⁴√m⁷ = 
d) ⁵√x⁶ = 
e) ⁷√a⁹ = 
f) √7⁵ = 
g) √2⁹ = 
h) ³√5¹⁰ = 
i) ⁴√7⁹ = 
j) ⁵√6⁸ = 

4) Fatore o radicando e simplifique os radicais:

a) √8 = 
b) √27 = 
c) ³√81 = 
d) ⁴√32 = 
e) √50 = 
f) √80 = 
g) √12 = 
h) √18 = 
i) √50 = 
j) √8 = 
k) √72 = 
l) √75 = 
m) √98 = 
n) √99 = 
o) √200 =


5) Calcule

a) √36 - √49 = 
b) ³√8 + √64 = 
c) -√100 - ³√64 = 
d) -³√125 - ³√-1 = 
e) ⁵√1 + √9 - ³√8 = 
f) √100 +⁵√-32 + ⁶√0 = 
g) ⁴√16 + ⁷√1 - ⁵√-1 = 

Propriedades dos radicais: exercícios resolvidos, teoria com exemplos

Para os radicais de radicandos positivos valem as seguintes propriedades:

1º Propriedade:

1) √49 = √7² = 7
2) ³√125 = ³√5³ = 5

Exemplos
a) √3² =3
b) ³√5³ = 5
c) ⁴√10⁴ = 10

2º Propriedade:

1) √4.25 = √100 = 10
2) √4 . √25 = 2 . 5 = 10

Comparando 1 e 2, temos √4.25 = √4 . √25

Exemplos

a) √2.7 = √2 . √7
b) √8.x = √8 . √x
c) ³√5.a = ³√5 . ³√a
d) ⁴√5.7.9 = ⁴√5 . ⁴√7 . ⁴√9

EXERCÍCIOS

7) Aplique a 1º propriedade:

a) √8² = 
b) ³√7³ = 
c) ⁵√x⁵ = 
d) √(7a)² = 
e) ³√(5x)³ = 
f) ⁴√(7x)⁴ = 
g) √(a²m)² = 
h) √(a + 3)² = 

8) Aplique a 2º propriedade:

a) √5 .7 = 
b) ³√2.8 = 
c) ³√5X = 
d) √10xy = 
e) √5x²m = 

3º) Propriedade

Exemplos

1) √4/25 = 2/5
2) √4/√25 = 2/5

Exercícios resolvidos

01. (UFCE) Simplificar a expressão:

Solução:

Exercício simples que se baseia na decomposição em fatores primos de cada radicando e da utilização da propriedade P1, como você pode observar no detalhamento a seguir. Tenha em conta que na soma ou subtração de radicais, cada parcela deve ser considerada isoladamente para se obter o resultado de uma expressão. Ou seja, não se aplica que a soma de duas raízes de mesmo índice é igual a raiz da soma, como é o caso do produto, por exemplo.

02. Calcular o quociente:

Solução:

Outro exercício de solução simples onde demonstro o uso das propriedades P1 e P3, e novamente, faço uso da decomposição em fatores primos dos radicandos:

03. Escrever em ordem de grandeza crescente os radicais:

Solução:

Para fazer a comparação entre os radicais devemos, inicialmente, reduzí-los ao mesmo índice. Isto é feito calculando o mínimo múltiplo comum (mmc) dos índices e, após, aplicando a propriedade P6. O mmc(2, 4, 3, 6) = 12 e reescrevendo os radicais (P6) vem:

Agora, basta considerar a ordem dos radicandos para estabelecer a ordem crescente dos radicais:

04. Efetuar

Solução:

Esboçada a seguir, onde utilizamos o fato de que o produto da soma pela diferença de dois números é igual ao quadrado do primeiro menos o quadrado do segundo (produto notável – PN) e as propriedades da Radiciação indicadas:

05. Simplifique a expressão:

 

a) -0,1

b) -1,7

c) -17

d) 0,1

e) 1,7

a) 0,4

b) 2,5

c) a

d) 1,5

e) 1

09. Escreva simplificadamente:

a) 

b) 

c) 

10) Calcule .

11)  Calcule .

12) Simplifique o radical 

13) (F. C. Chagas-SP) O número  √2352 corresponde a:

a) 4  √7 .
b) 4  √21 .
c) 28  √3 .
d) 28  √21 .
e) 56  √3 .

14) (UFSC) O valor de  x, que satisfaz a equação  22x + 1 – 3 . 2x + 2 = 32, é:

15) (Fuvest)    é igual a:

16) (UFSC)  Dê o somatório da(s) proposição(ões) VERDADEIRA(S).

Gabarito:

06) A  07) B  08) B  09)  a) 

b)           c)    

10) 25     11) 49    12)    14) x = 3   15) E
16) 2 + 8 + 16 + 64 = 90

Radicais como potências de expoente fraccionário: exercícios, teoria e exemplos

       

             

Com a>0, n ∈ ℕ e m/n ∈ℚ  

                

Exemplos:

                        ⁵√2^-3 = 2^-3/5

                        3⁵ =3 ^15/3 = ³ √(3 ¹⁵)       

                       2 ^–1/4 = (1/2)^1/4 = ⁴√(1/2) ou 2^-1/4 =⁴√2^-1

Se 3 é um número real positivo e 2/4 é um número racional, com 2 e 4 inteiros definimos:

Exemplos

a) (2²⁾⁴ = ⁴√2²
b) (5³⁾⁴ = ⁴√5³
c) (7¹⁾² = √7

EXERCÍCIOS

1) Escreva em forma de potência com expoente fracionário:

a) ³√7² = 
b) ⁵√a³ = 
c) √10 = 
d) ⁴√a³ = 
e) √x⁵ = 
f) ³√m = 

2) Escreva em forma de radical:

a) 5³⁾⁴ = 
b) 5¹⁾² = 
c) a²⁾⁵ = 
d) a¹⁾³ = 
e) 2⁶⁾⁷ = 
f) 6¹⁾² = 


3) Resolva como os exemplos: