Doutor Matemático: Operações com monômios conceitos e exercícios

Monômio

É uma expressão algébrica que apresenta apenas a multiplicação do coeficiente com a parte literal, como por exemplo:

$2x$
$4ab$
$10x^2$
$20xyz$
$y$
$b^4$
$100b^2x^3$

Monômios semelhantes

São monômios que apresentam as partes literais idênticas, como por exemplo:

$2y \text{ e } 4y$
$7x^2 \text{ e } 8x^2$
$10ab^2c^4 \text{ e } 25ab^2c^4$
$y \text{ e } 55y$

Adição e subtração de monômios

Apenas podemos somar e subtrair monômios semelhantes, como por exemplo:

$2a + 7a = 9a$
$5x -2x = 3x$
$10ab - 9ab = ab$
$7bc + 3cb = 10bc \text{ ou } 10cb$
$-12xy - 10xy = -22xy$
$7a^2b - 2a^2b = 5a^2b$
$17b^3c^4 - 3b^3c^4 = 14b^3c^4$
$x^3y^4z^7 + 10x^3y^4z^7 = 11x^3y^4z^7$

1) (EAM – Aprendiz de marinheiro) Analise a figura a seguir:

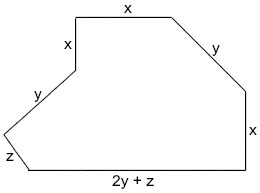
Suponha que o terreno comprado por um proprietário tenha a forma da figura acima e suas medidas sejam representadas, em unidades de comprimento, pelas variáveis X, Y e Z. A expressão algébrica que representa o perímetro desse terreno é:

a) 2x + 3y + z

b) 3x + 4y + 2z

c) 3x + 3y + z

d) 3x + 2y + 3z

e) 4x + 3y + 2

2) Resolva: (y² + 4y – 5) + (– 3y² + 12y – 1).

3) Subtraia x² + 12x – 9 por – 8x² + 7x – 1

4) Efetue as seguintes adições:

a) (2x²-9x+2) + (3x²+7x-1)

b) (5x²+5x-8) + (-2x²+3x-2)

c) (3x-6y+4) + (4x+2y-2)

d) (5x²-7x+2) + (2x²+7x-1)

5) Efetue as seguintes subtrações:

a) (5x²-4x+7) - (3x²+7x-1)

b) (6x²-6x+9) - (3x²+8x-2)

c) (7x-4y+2) - (2x-2y+5)

d) (4x-y-1) - (9x+y+3)

Valor numérico de uma expressão algébrica:

1) Calcule o valor numérico das expressões:

a) x – y (para x =5 e y = -4)
b) 3x + a (para x =2 e a=6)
c) 2x + m ( para x = -1 e m = -3)
d) m – 2 a ( para m =3 e a = -5)

Multiplicação de monômios

Para multiplicarmos monômios, seguimos os passos:

Multiplicar os coeficientes;
Agrupar as letras que não forem comuns aos dois monômios;
Somar os expoentes das letras que forem comuns aos dois monômios.

Exemplos:

$2x \cdot 2x = 4x^2$
$4xy \cdot 6xy^2 = 24x^2y^3$
$10a^2b \cdot 9a^2b^3 = 90a^4b^4$
$5xyz \cdot 6x^2y^3 = 30x^3y^4z$
$2x \cdot 3y = 6xy$
$4ab \cdot 5z = 20abz$

Divisão entre monômios

Para dividirmos monômios, seguimos os passos:

Dividir o do monômio do numerador pelo coeficiente do monômio do denominador;
Preservar as letras do monômio do numerador;
Subtrair os expoentes das letras agrupadas pelos expoentes das letras comuns do denominador;
Agrupar as letras que não forem comuns aos dois monômios, com expoente negativo.

Exemplos:

$\frac {5x^3}{5x^2} = x$

$\frac {10x^2y^2}{2x} = 5xy^2$

$\frac{30z}{5z} = 6$

$\frac{20b^3}{10b} = 2b^2$

$\frac {10x^2y^2z^3}{2x5z^2} = xy^2z$

$\frac{22z}{11zy^2} = 2y^{-2}$

$\frac{20a^6b^3c^9}{5a^2b^{-1}c^5} = 4a^4b^4c^4$

Potenciação de monômios

A potenciação é outra operação que podemos fazer com os monômios, sendo possível aplicar todas as propriedades usuais das potências e das multiplicações.

Com frequência são usadas as seguintes propriedades de potências:

Potência de um produto: $(a \cdot b)^n = a^n \cdot b^n$
Potência de potência: $(a^n)^m = a^{n.m}$

Para uma potência de monômio siga os passos:

Reescrever o monômio usando a potência de um produto. Isso fará com que cada literal tenha como expoente o expoente original do literal mutilplicado pela potência do monômio.
Calcular os novos expoentes dos literais, usando a potência de produto, isto é, multiplicando os expoentes.

Exemplos:

$(2xyz)^2 =$
$2^2x^2y^2z^2 =$
$4x^2y^2z^2 =$

$(7x^2y^3)^3 =$
$7^3(x^2)^3(y^3)^3 =$
$343x^{2 \cdot 3}y^{3 \cdot 3} =$
$343x^6y^9 =$

$(5a^2b^3c^4x^5y^6z^7)^3 =$
$5^3(a^2)^3(b^3)^3(c^4)^3(x^5)^3(y^6)^3(z^7)^3 =$
$5^3a^{2 \cdot 3}b^{3 \cdot 3}c^{4 \cdot 3}x^{5 \cdot 3}y^{6 \cdot 3}z^{7 \cdot 3} =$
$125a^6b^9c^{12}x^{15}y^{18}z^{21} =$