
Da mesma forma que ocorre com os números, podemos executar as operações básicas com os radicais: adição, subtração, multiplicação, divisão, potenciação e radiciação
Adição e subtração: os radicais não são semelhantes
Neste caso, tiramos as raízes de cada termo e somamos ou subtraímos os resultados. Observe os exemplos abaixo:
a)
b)
Adição e subtração: os radicais são semelhantes
Basta somar ou subtrair os números que multiplicam o radical. Observe os exemplos abaixo:
a)
b)
Adição e subtração: os radicais tornam-se semelhantes depois de simplificados
Este é o caso mais complexo, pois é necessário simplificar os radicais. Observe o exemplo abaixo:
;
;
Redução de radicais ao menor índice comum
Reduzir ao mesmo índice comum.
Para isso, calculamos o m.m.c. dos índices e dividimos o m.m.c. pelos índices de cada radical e multiplica-se o quociente obtido pelo expoente do radicando.
O m.m.c. dos índices
, e vale .
Dividimos o número (novo índice comum) pelos índices de cada radical e multiplica-se o quociente obtido pelo expoente do radicando.
Multiplicação e divisão: os radicais têm o mesmo índice
Neste caso, basta multiplicar ou dividir os radicandos.
a)
b)
Multiplicação e divisão: os radicais não tem o mesmo índice
Neste caso, é necessário reduzi-los ao mesmo índice.
=
Potenciação de radicais
Neste caso, basta elevar o radicando a potência. Observe o exemplo abaixo:
Podemos generalizar o exemplo acima:
Radiciação
Neste caso, temos uma raiz “dentro” de outra raiz. Assim, basta multiplicar os índices de todas as raízes. Observe o exemplo abaixo:
Os índices e são multiplicados e o índice final é ().
Podemos generalizar o exemplo acima:
Exercícios:
1. Calcule o valor da expressão:
![]()
Resolução
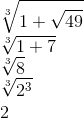
2. Calcule o valor da expressão:
![]()
Resolução
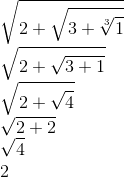
3. Simplifique a expressão:
![]()
Resolução
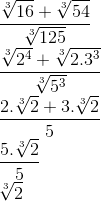
4. Ache o resultado da expressão:
![]()
Resolução
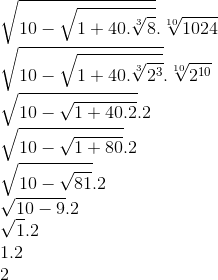


Nenhum comentário:
Postar um comentário