Exercícios sobre ângulos: correspondentes, colaterais internos e externos, alternos internos e externos.

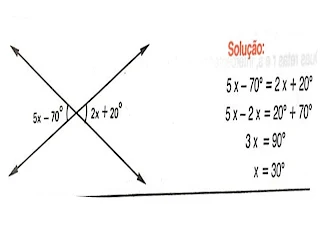
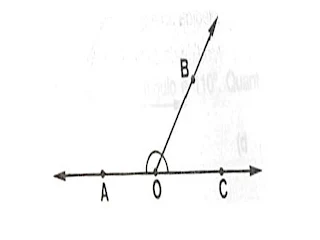
Duas retas r e s, interceptadas  pela transversalo t, formam oito ângulos.

Os pares de ângulos com um vértice em A e o outro em B são assim determinados:

= Correspondentes: 1 e 5, 4 e 8, 2 e 6, 3 e 7

= Colaterais Internos: 4 e 5, 3 e 6

= Colaterais externos: 1 e 8, 2 e 7

= Alternos internos: 4 e 6, 3 e 5

= Alternos externos: 1 e 7, 2 e 8

ILUSTRANDO:

= ALTERNOS (um de cada "lado" da transversal).

= COLATERAIS (ambos do mesmo "lado" da transvwesal)

EXERCÍCIOS

1) Dê o nome dos pares de ângulod de acordo com a figura:

a) a e g

b) a e e

c) d e h

d) c e g

e) c e e

f) a e f

g) b e h

h) b e f

i) d e f

j) c e e

l) c e h

m) b e e

PROPRIEDADES

Considere duas retas paralelas e uma transversal.

 

Medindo esses ângulos com o transferidor, você vai concluir que são validas as seguintes propriedades:

= Os ângulos correspondentes são congruentes
= Os ângulos alternos externos são congruentes
= Os ângulos alternos internos são congruentes.
= Os ângulos colaterais externos são suplememntares.
= Os ângulos colaterais internos são suplementares

EXERCÍCIOS

1)  Sabendo que r//s, determine a medida dos ângulos indicados:

a)

b)

c)

d)

2) Sabendo que r // a , calcule x:

a)

b)

c)



Exercícios sobre ângulos opostos pelo vértice

Duas retas concorrentes determinam quatro ângulos, dois a dois , opostos pelo vértice

Na figura:

â e  c são opostos pelo vértice.

m e n são opostos pelo vértice

TEOREMA

Dois ângulos opostos´pelo vértice são congruentes.

prova:

Sejam os ângulos a e b opostos pelo vértice.

1) m(â) + m(^c) = 180°

2) m(b) + m(c) = 180°

comparando : m(â) + m(c) = m(b) + m(c)

m(â) = m(b)

Se a e b têm a mesma medida, eles são congruentes.

EXECÍCIOS

1) Quais são os 3 pares de ângulos opostos pelo vértice?

2)  Se x = 50° , determine y, m e n:

3) Calcule os ângulos x,y, z e w da figura:

4) Calcule os ângulos x, y e z das figuras:

5) Calcule x:

6) Calcule x:

7) Calcule x :

8) Calcule x:

9) As medidas de dois ângulos opostos pelo vértice são expressas em graus por  15x - 14° e 3x + 10°. Quanto vale x?

10) As medidas de dois ângulos opostos pelo vértice são expressas em graus por (2m - 50) e (m + 35). Quanto vale m?

Exercícios sobre ângulos suplementares somam 180º

Dois ângulos são suplementares quando a soma de suas medidas é 180°

m(AÔB) + m(BÔC) = 180°

Exemplos:

= 50° e 130° são angulos suplementares, porque 50° + 130° = 180°

= 125° e 55° são ângulos suplementares, porque 125°  + 55º = 180°

EXERCÍCIOS

1) Responda:

a) Um ângulo de 70° e um de 110° são suplementares?
R: (

b) Um ângulo de 155° e um de 25° são suplementares?

2) Calcule o suplemento dos seguintes ângulos:
a) 30° = (R:
b) 85° = (R: 
c) 72° = (R: 
d) 132° 30´ = (R: 
e) 140° 20´ = (R: 
f) 151° 40` =(R:


3) Determine x, sabendo que os ángulos são suplementares:

4) Determine x, sabendo que os ângulos são suplementares:



5) Calcule x:

6) A quarta parte da medida de um ângulo mede 30°. Calcule a medida do seu suplemento.

7) A medida de um ângulo é igual à medida de seu suplemento. Calcule esse ângulo.

8) Calcule a medida de um ângulo que é igual ao triplo de seu suplemento.

9) O dobro da medida de um ângulo é igual à medida do suplemento desse ângulo. Calcule a medida do ângulo.

10) O triplo da medida de um ângulo mais a medida do suplemento desse ângulo é 250°. Calculo a medida do ângulo.

11) Calcule a medida de um ângulo cuja medida é igual a 2/3 do seu suplemento.

12) A soma do complemento com o suplemento de um ângulo é 110° . Quanto mede o ângulo?

Exercícios sobre ângulos complementares somam 90°

ÂNGULOS COMPLEMENTARES

Dois angulos são complementares quando am soma de suas medidas é 90°

m(AÔB) + m((BÔC) = m(AÔC)

Exemplos:

 65° e 25° são ângulos complementares , porque 65° + 25° = 90°

EXERCÍCIOS 

1) Responda: 

a) Um ângulo de 20° e um de 70° são complementares?
b) Um ângulo de 35° e um de 65° são complementares?
c) Um ângulo de 73° e um de 27° são complementares?
d) Um ângulo de 58° e um de 32° são complementares?


2) Calcule o complemento dos seguintes ângulos:

a) 34°
b) 72°
c) 84°
d) 18° 25´
e) 40° 30´
f) 51° 20´

3) Resolva as equações abaixo, onde a inc´gnita x é um ângulo (medido em graus)

a) 2x = 90°
b) x + 17° = 90°
c)  4x + 10° = 90°
d) x + 8x = 90°
e) 5x - 20° = 1° = 2x
f) x = 2( 90° - x)
g) 4( x + 3° 0 = 20°
h) ( 3x - 20° ) + 50° = 90°
I) 3( x + 1°) = 2( x  + 7°)
J) 2x + 2 (x + 1° ) = 4° + 3 ( x + 2°)

4) Determine x, sabendo que os ângulos são complementares:

5) Dado um ângulo de medida x, indicar:

a) o seu complemento.

b) o dobro do seu complemento

c) o triplo do seu complemento.

d) a metade do seu complemento

e) a terça parte do seu complemento

7) A medida de um ângulo é igual à medida de seu comprimento, quanto mede esse  ângulo?

8) A medida de um ângulo é a metade da medida do seu comprimento. Calcule a medida desse ângulo.

9) Calcule a medida de um ângulo cuja medida é igual ao triplo de seu complemento.

10) A diferença entreo o dobro da medida de um ângulo e o seu complemnto é 45° Calcule a medida desse ângulo.

11) A terça parte do complemento de um ângulo mede 20°. Qual a medida do ângulo?

12) Dois ângulos complementares têm suas medidas expressas em graus por 3x + 25° e 4x - 5° . Quanto medem esses ângulos?