“Divisão e Conquista: é uma técnica valiosa usada em momentos complicados, onde dividimos um grande problema em problemas menores até ser resolvido". Anatolii Karatsuba
terça-feira, 24 de março de 2020
domingo, 3 de setembro de 2017
Probabilidade
Na matemática, a probabilidade permite obter o cálculo das ocorrências possíveis num experimento aleatório (fenômeno aleatório). Em outras palavras, a probabilidade analisa as “chances” de obter determinado resultado.
A teoria das probabilidades inclui conceitos matemáticos que foram explorados já na antiguidade. O termo derivado do latim “probare” corresponde ao verbo provar ou testar.
Experimento Aleatório
O experimento ou evento aleatório é aquele que pode ocorrer e resultar de diferentes maneiras cada vez que é lançado. Ou seja, não sabemos seu resultado, porém podemos calcular quais resultados possíveis podemos obter.
Por exemplo, podemos citar um dado, com 6 faces, donde cada face é um número de 1 a 6.
Fórmula da Probabilidade
Assim, se num fenômeno aleatório as possibilidades são igualmente prováveis, a probabilidade de ocorrer um evento é medida pela divisão entre o número de eventos favoráveis e o número total de resultados possíveis:
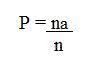
Donde
P: probabilidade
na: número de casos (eventos) favoráveis
n: número de casos (eventos) possíveis (total)
na: número de casos (eventos) favoráveis
n: número de casos (eventos) possíveis (total)
Espaço Amostral
Representado pela letra S, o espaço amostral corresponde ao conjunto de resultados possíveis obtidos a partir de um evento ou fenômeno aleatório.
Por exemplo num baralho de cartas, onde o espaço amostral corresponde às 52 cartas que compõem o baralho.
Da mesma forma, o espaço amostral no lançamento de um dado, são as seis faces que o compõem: S = {1, 2, 3, 4, 5 e 6}.
Note que os subconjuntos de um espaço amostral são denominados “eventos”, ou seja, no conjunto de cartas, há 52 eventos possíveis, enquanto no dado há seis.
Assim, podemos concluir que a probabilidade é calculada pela divisão de eventos pelo espaço amostral.
Exercícios Resolvidos
1. Se lançarmos um dado de 6 faces, qual a probabilidade de sair o número seis?
Segundo a teoria da probabilidade, ela é calculada pela divisão entre o número de eventos favoráveis e o número de eventos possíveis, nesse caso:
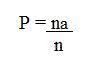
na (casos favoráveis): 1 lado (lado seis)
n (casos possíveis) : 6 lados
n (casos possíveis) : 6 lados
Logo,
P = 1/6
P = 0,166 ou 16,6%
P = 0,166 ou 16,6%
2. O baralho de cartas é formado por 52 cartas divididas em quatro naipes (copas, paus, ouros e espadas) sendo 13 cartas de cada naipe. Dessa forma, se retirar uma carta do baralho, qual a probabilidade de sair uma carta do naipe de paus?
Segundo a teoria da probabilidade, devemos obter o número de evento favoráveis e possíveis, para assim, calcular, através da fórmula:
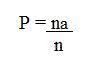
na: 13 (total de cartas do naipe de paus)
n: 52 (total de cartas do baralho)
n: 52 (total de cartas do baralho)
Logo,
P = 13/52
P = 0,25 ou 25%
P = 0,25 ou 25%
Probabilidade condicional
- Assim, temos que os eventos A e B de um espaço amostral finito e não vazio (Ω) pode ser expresso da seguinte maneira:
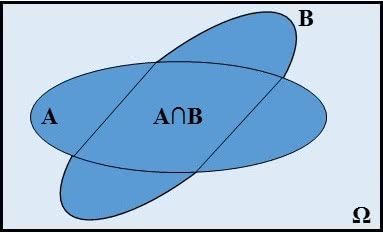
Uma outra maneira de expressar a probabilidade condicional dos eventos é dividindo o numerador e o denominador do segundo membro por n(Ω) ≠ 0:

sexta-feira, 16 de junho de 2017
Exercícios Princípio fundamental da contagem com resposta
1) Thiago possui 3 blusas diferentes e 2 calças diferentes. De quantas maneiras ele poderá escolher uma blusa e uma calça para se vestir? Resposta: 6
2) Quantos números de dois algarismos podem ser formados utilizando elementos do conjunto {1, 2, 3}? Resposta: 9
3) Quantos números de dois algarismos diferentes (distintos) podem ser formados utilizando elementos do conjunto {1, 2, 3}? Resposta: 6
4) Quantos números de três algarismos podem ser formados utilizando elementos do conjunto {1, 2, 3}? Resposta: 27
5) Quantos números de três algarismos diferentes (distintos) podem ser formados utilizando elementos do conjunto {1, 2, 3}? Resposta: 6
6) Um estádio possui 4 portões. De quantas maneiras diferentes um torcedor pode entrar e sair desse estádio? Resposta: 16
7) Um estádio possui 4 portões. De quantas maneiras diferentes um torcedor pode entrar e sair desse estádio utilizando, para sair, um portão diferente do que entrou? Resposta: 12
8) Mariana desenhou uma bandeira retangular de 3 listras e deseja pintá-la, de modo que duas listras consecutivas não sejam pintadas da mesma cor. Se ela possui 4 lápis de cores diferentes, de quantas maneiras poderá pintar sua bandeira? Resposta: 36
9) Numa prova havia 4 itens para que os alunos respondessem V (verdadeiro) ou F (falso). De quantas maneiras diferentes um aluno que vai “chutar” todas as repostas poderá responder esses itens? Resposta: 16
10) Um painel luminoso retangular é composto por 5 lâmpadas. De quantas maneiras diferentes esse painel pode estar iluminado? (considera-se o painel iluminado se, pelo menos, uma de suas lâmpadas estiver acesa) Resposta: 31
11) Quantos numeros de 3 algarismo distintos podem ser formados usando-se os algariasmo 1,2,3,4 e 5?
12) Um restaurante ofereçe no cardapio 2 saladas distintas,e 4 tipodes de pratos de carne,5 variedades de bebidas e 3 sobremesas diferentes. Uma pessoa deseja uma salada,um prato de carne,uma bebida e uma sobremesa.De quantas maneiras a pessoa podera fazer seu pedido?
13) Quatro times de futebol(Vasco,Atletico,Corinthians e Internacional ) disputam um torneio.Quantos e quais são as possibilidades de classificação para os três primeiros lugares?
14) Numa eleição de uma escolahá 3 candidatos a presidente,cinco a vice-presidente,¨a secretario e 7 a tesoreiro.Quantos podem ser os resultados da eleição?
EXERCÍCIOS COMPLEMENTARES
15) Com os algarismos 1, 2, 3, 4, 5 e 6, quantos números de três algarismos distintos podemos formar?
a) 30 b) 60 c) 90 d) 120 e) 150
16) Uma prova consta de 10 questões do tipo V ou F. De quantas maneiras distintas ela pode ser resolvida?
a) 128 b) 256 c) 512 d) 1024 e) 2048
17) Quantos números de três algarismos podemos com os algarismos 0, 1, 2, 3, 4, 5, 6 e 7?
a) 348 b) 448 c) 548 d) 648 e) 748
18) Quantos números ímpares de três algarismos distintos podemos formar com os algarismos 0, 1, 2, 3, 4, 5, 6 e 7?
a) 72 b) 144 c) 200 d) 240 e) 288
19) Um jantar constará de três partes: entrada, prato principal e sobremesa. De quantas maneiras distintas ele poderá ser composto, se há como opções oito entradas, cinco pratos principais e quatro sobremesa?
a) 160 b) 150 c) 120 d) 80 e) 17
20) Se um quarto tem 5 portas, o número de maneiras distintas de se entrar nele e sair dele por um porta diferente é:
a) 5 b) 10 c) 15 d) 20 e) 25
21) Quantos números de 4 algarismos diferentes têm o algarismo da unidade de milhar igual a 3?
a) 1512 b) 1008 c) 504 d) 3024 e) 2520
22) Cinco sinaleiros estão alinhados. Cada um tem três bandeiras: uma amarela, uma verde e uma vermelha. Os cinco sinaleiros levantam uma bandeira cada, ao mesmo tempo, transmitindo-se assim um sinal. A quantidade de sinais diferentes que se pode transmitir é:
a) 15 b) 125 c) 243 d) 1215 e) 729
23) Com os algarismos 1, 2, 3, 4, 5 e 6 são formados números de quatro algarismos distintos. Dentre eles são divisíveis por 5:
a) 20 números b) 30 números c) 60 números d) 120 números e) 180 números
24) Uma estrada de ferro tem 10 estações. Quantos tipos distintos de bilhetes existem em circulação, sabendo-se que cada bilhete contém impressos apenas a estação de partida e a estação de chegada? (Supondo que o trem tem vagões de apenas uma classe)
a) 28 b) 45 c) 20 d) 56 e) 90
GABARITO COMPLEMENTARES
15- D
16- D
17- B
18- B
19- A
20- D
21- C
22- C
23- C
24- B
http://www.matematiques.com.br
Assinar:
Comentários (Atom)
Destaque!!!!!!!!!!!
Aula criativa de matemática sobre a conversão do dólar
Um emprego em um navio de cruzeiro pode ser uma grande chance de conhecer lugares novos e ganhar um bom salário. Quanto melhor for seu ingl...

-
O objeto capaz de medir o valor de um ângulo é chamado de transferidor, podendo ele ser de “meia volta” (180º) ou volta inteira (360º). ...
-
Frações: Própria, imprópria, aparente e números mistos. Temos que ter a noção básica de que toda fração é uma divisão. E que uma f...
-
A potenciação é uma multiplicação de fatores iguais Exemplos: 1) (1,2)² = 1,2 x 1,2 =1,44 2) (0,4)³ = 0,4 x 0,4 x 0,4 = 0,064 vamo...