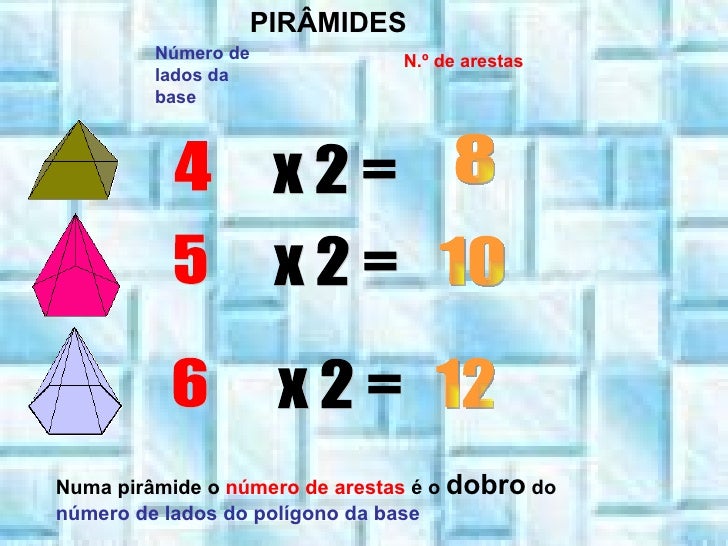
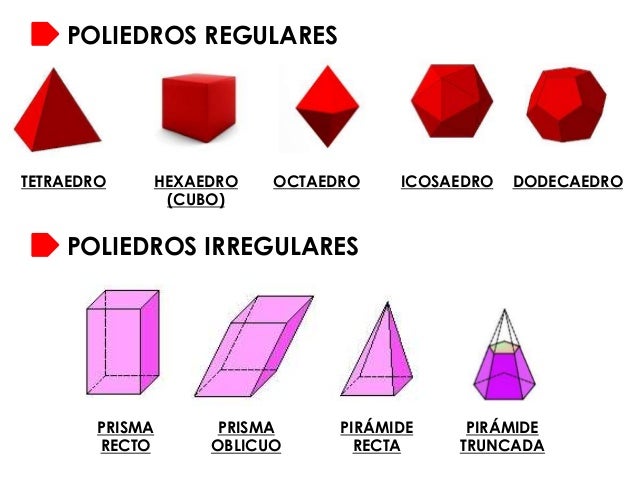
Um prisma é caracterizado como um sólido que possui duas bases idênticas e paralelas. Ele é classificado de acordo com o formato de sua base e de acordo com o ângulo que as laterais formam com as bases. Mas independente do tipo do prisma que estamos lidando, é possível realizar sua planificação, isto é, reconstruir um sólido como uma figura plana. Podemos imaginar esse processo semelhante ao ato de abrir uma caixa ou mesmo como o processo de embalar uma caixa para presente;
1) Como encontrar a área total de um prisma?
Devemos calculá-la em etapas. Primeiramente devemos encontrar o valor da área da base. Para isso, basta um só calculo, pois as bases são idênticas. A área da base deve ser multiplicada por dois, pois sempre haverá duas bases em um prisma. Feito isso, devemos encontrar a área lateral, verificando as medidas de um retângulo da lateral para calcular sua área. Então, multiplicamo-la pela quantidade de retângulos que compõem a lateral. Dessa forma, a área de um prisma será dada por:
At = Al + 2.Ab
At é a área total do prisma;
Al é a área lateral;
Ab é a área da base.

Al é a área lateral;
Ab é a área da base.
O volume do prisma é calculado pela multiplicação entre a área da base e a altura.
O volume determina a capacidade que possui uma figura geométrica espacial. Vale lembrar que, geralmente, ele é dado em cm3(centímetros cúbicos) ou m3 (metros cúbicos).
2) Como Calcular o volume do prisma?
Para calcular o volume do prisma utiliza-se a seguinte expressão:
V = Ab.h
Onde,
Ab: área da base
h: altura
h: altura
Obs: Não se esqueça que para calcular a área da base é importante saber o formato que a figura apresenta. Por exemplo, num prisma quadrangular a área da base será um quadrado. Já num prisma triangular, a base é formada por um triângulo.

1) Em um prisma regular triangular, cada aresta lateral mede 10 cm e cada aresta da base mede 6 cm. Calcular desse Prisma:
a) a área de uma face lateral.
Af = (6.10) cm²
Af = 60 cm²
b) a área de uma base.
Cada base é um triângulo equilátero de lado 6 cm. Lembrando que a altura h de um triângulo equilátero de lado a é dada por

Portanto, a área B de uma base é:
c) a área lateral.
A área lateral AL é a soma das áreas das três fases laterais, isto é:
AL = 3 . Af
AL = 3 . 60 cm²
AL = 180 cm²
d) a área total.
A área total At é a soma da área lateral AL com duas vezes a área B de uma base, isto é:
At = AL + 2B
At = (180 + 18 √3) cm²
2) Um prisma reto de altura 10 cm tem como polígonos das bases triângulos retângulos de catetos 3 cm e 4 cm. Calcule a área total desse prima.
Resolução:
3)Em uma piscina regular hexagonal cada aresta lateral mede 8 dm e cada aresta da base mede 4 dm. Calcule, desses prisma:
a) a área de cada face lateral;
Af = b . h
Af = 4 .8
Af = 32 dm²
b) a área de uma base;
Ab = (6.10 √3) / 4
Ab = 24 √3 dm²
c) a área lateral;
AL = 6.4.8
AL = 192 dm²
d) a área total;
At = 2.24 √3 +192
At = 48 √3 + 192 dm²
Diagonais do Paralelepípedo
1) As dimensões de um paralelepípedo reto-retângular são 20 cm, 12 cm e 9 cm.Calcular a medida de uma diagonal desse paralelepípedo.

Resolução:
D = √a² + b² + c²
D = √20² + 12² + 9²
D = √400 + 144 + 81
D = √625
D = 25 cm²
2) O comprimento EA, a largura EH e a altura EF do paralelepípedo reto-retângulo representado ao lado são 12 cm, 3 cm e 4cm, respectivamente, calcule:


a) A medida de uma diagonal da face EFGH;
D = √3²+4²
D = √9 + 16
D = √25
D = 5 cm²
b) A medida de uma diagonal do paralelepípedo;
D = √3² + 4² + 12²
D = √9 + 16 + 144
D = √169
D = 13 cm²
c) a área total do paralelepípedo;
A1 = 12 . 3 A2 = 4.3 At = A1 + A2
A1 = 36 A2 = 12 At = 144 + 24
A1 = 4.36 A2 = 2.12 At = 168 cm²
A1 = 144 A2 = 24
d) o volume do paralelepípedo;
V = b.h.l
V = 12.3.4
V = 169 cm³
Cubo
1) A área total de um cubo é 54 cm². Calcule a medida da diagonal desse cubo.
Resolução:
At = 6a² d = a√3
54 = 6a² d= 3√3cm²
54 /6 = a²
a = √9
a =3 cm
2) A diagonal de um mede √75 cm .Calcule a área total desse cubo:
Resolução:
d = √75
d = L√3
√75 = L√3
5√3 = L√3
L = (5√3) / √3
L = 5 cm
3) Se a soma das medidas de todas as arestas de um cubo é 60 cm,então o volume desse cubo, em centímentros cúbicos, é:
a) 125 cm³
b) 100 cm³
c) 75 cm³
d) 60 cm³
e) 25 cm³
Resolução:
12 arestas
60 cm / 12 = 5
V = 5³ = 125 cm³
Letra a) 125 cm³
4)(UFSCar SP/2016) Uma caixinha de papelão tem a forma de um prisma reto de base quadrada, com 6 cm de lado e altura h, conforme mostra a figura.
Sabendo que o volume dessa caixinha é 288 cm3, pode-se concluir corretamente que o valor da sua área lateral, em centímetros quadrados, é
a) 192.
b) 170.
c) 154.
d) 128.
e) 96.
Solução:
A estratégia para obter a área lateral desse prisma é calcular primeiramente a medida de sua altura. Como foi dada a medida do volume, podemos usar a fórmula para o cálculo do volume de um prisma para descobrir essa medida que falta.
Para tanto, o volume de um prisma é dado pelo produto da área da base pela altura. Sendo assim, a fórmula é:
V = Ab·h
A base desse prisma é um quadrado, portanto, sua área é dada pelo quadrado da medida do lado. Assim, Ab = 62 = 36. Substituindo esse valor e a área da base na expressão acima, teremos:
288 = 36·h
36·h = 288
h = 288
36
36
h = 8 cm
A área lateral é dada pela soma das áreas das faces laterais. Como são todas congruentes, basta calcular uma e multiplicar o resultado por 4:
Al = 4·6·8 = 4·48 = 192 cm2
Gabarito: letra A.