Relembrando a geometria plana : Polígonos
Em geometria, uma figura plana (duas dimensões) com três ou mais lados. Os polígonos comuns têm nomes que definem o número de lados (por exemplo, triângulo, quadrilátero, pentágono).
Polígonos regulares
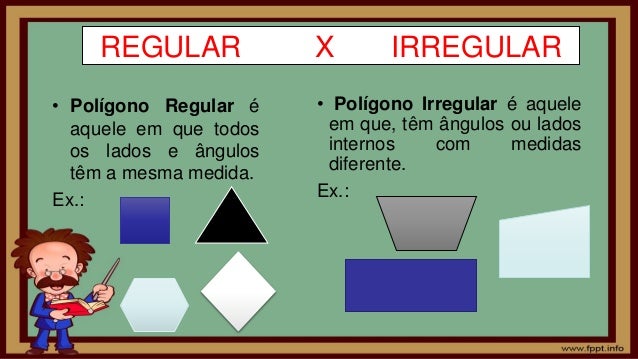
Obs. Estas figuras são regulares pois temos lados e ângulos internos congruentes, ou seja, eles são equiláteros e equiângulo.
Polígonos regulares

Obs. Estas figuras são regulares pois temos lados e ângulos internos congruentes, ou seja, eles são equiláteros e equiângulo.
Na figura abaixo temos um polígono convexo e outro não convexo.

Agora vamos falar de figuras em 3 dimensões:



Na Geometria Espacial temos Poliedros convexos e côncavos

*Convexo : quando qualquer segmento de reta ficará inteiramente contido no poliedro.
*Não convexo ou côncavo é quando algum segmento de reta não está inteiramente contido no poliedro.


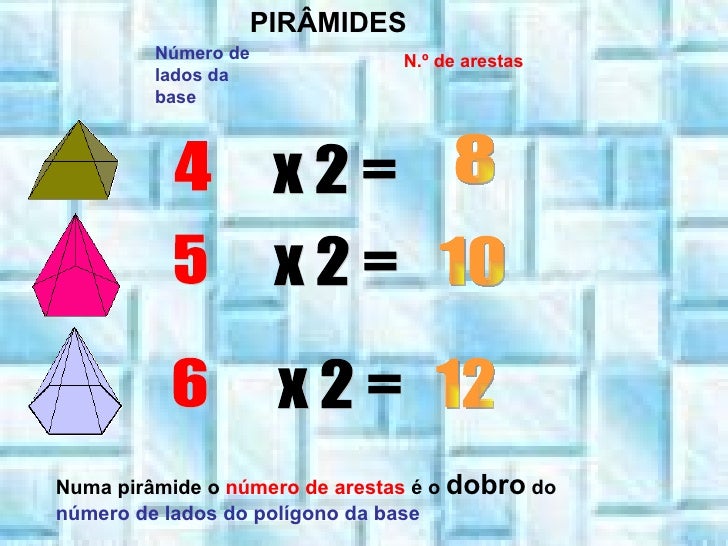
Aplicando essa relação em alguns exemplos:

Em um poliedro, também podemos relacionar que o número de lados é igual ao dobro do número de arestas, assim:
Onde N = número de lados e A = número de arestas.
Ou de outo modo temos:
A = N/2
Para calcular a soma das medidas dos ângulos internos das faces de um poliedro sabendo somente o número de arestas utilize a relação que segue:
S = soma dos ângulos internos
V = vértices
Por exemplo:

Dados 8 vértices de um cubo, calcule a soma de seus ângulos internos.
Resposta:
S = 360º . (8 - 2) = 2160º
.
Agora essa famosa relação serve para todo poliedro convexo:

ou dessa forma:

Aplicando essa relação em alguns exemplos:

Em um poliedro, também podemos relacionar que o número de lados é igual ao dobro do número de arestas, assim:
N = 2. A
Ou de outo modo temos:
A = N/2

S = 360º . ( V - 2)
Onde:S = soma dos ângulos internos
V = vértices
Por exemplo:
Dados 8 vértices de um cubo, calcule a soma de seus ângulos internos.
Resposta:
S = 360º . (8 - 2) = 2160º
.
Poliedros Regulares e irregulares
*No poliedro regular teremos todas as faces polígonos regulares congruentes entre si e de cada vértice parte o mesmo números de arestas.

*Já no poliedro irregular os polígonos das faces não são congruentes.

*Já no poliedro irregular os polígonos das faces não são congruentes.
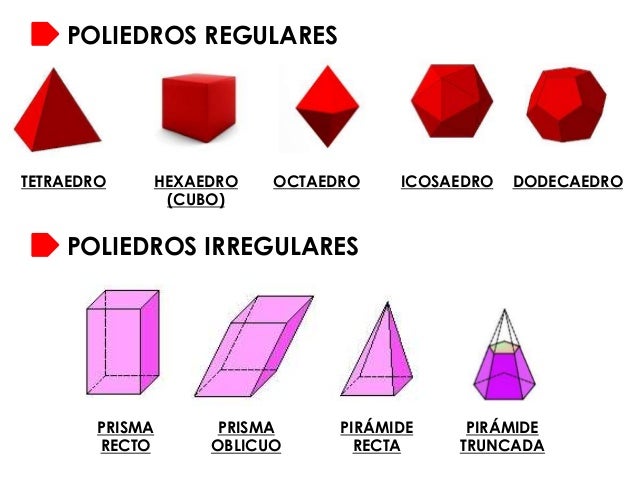
Note essas três fórmulas para vocês calcularem Face (F), Aresta (A) e Vértice (V) somente para os poliedros convexos regulares: tetraedro regular, cubo, octaedro regular, dodecaedro regular e icosaedro regular como podem visualizar abaixo:
Veja a tabela dos cinco poliedros convexos regulares e algumas fórmulas para calcular Face (F), Aresta (A) e Vértice (V) de cada um deles tendo n = lados e p = arestas.

Agora a tabela dos cinco poliedros convexos regulares e suas planificações:




Nenhum comentário:
Postar um comentário