CONCEITO
QUADRILÁTERO é um poligono de quatro lados.
No quadrilátero ao abaixo destacamos:
- Vértices: A, B, C, D
- Lados : AB, BC, CD e DA
- Ângulos internos : A, B, C, e D
- Lados opostos : AB e CD, AD e BC
- Ângulos opostos : A e C, B e D
Lembre-se de que um quadrilatero é convexo quando qualquer sgmento com extremeidades no quadrilatero está contido nele.
Estudaremos apenas os quadriláteros convexos.
DIAGONAL
O segmento que une dois vértices não consecutivos é chamado diagonal.
Na figura, AC e BD são diagonais.
EXERCÍCIOS
1) Observe o quadrilátero e responda:
a) Quais são os lados ?
b) Quais são os vértices?
c) Quais são os ângulos internos?
d) Quais são as diagonais indicadas?
2) Considere o quadrilátero ABCD
a) Nomeie os dois pares de lados oposto.
b) Nomeie os dois pares de ângulos opostos.
3) Perímetro de um quadrilátero mede 41 cm . Quanto mede cada lado se as medidas são representadas por x, x + 2, 3x + 1 e 2x -4?
SOMA DOS ÂNGULOS INTERNOS DE UM QUADRILÁTERO
ABCD é um quadrilátero convexo e a diagonal AC o divide em dois triângulos
veja:
A soma dos ângulos internos dos dois triângulos é a soma dos ângulos internos do quadrilátero, logo:
A soma dos ângulos internos de um quadrilatero é : 180° + 180° = 360°
EXERCICIOS
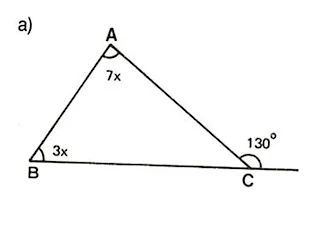
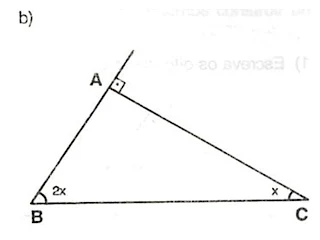
4) Calcule o valor de x nos quadrilateros;
5) Calcule o valor de x nos seguiontes quadrilateros:
6) Calcule o valor de x nos quadriláteros:
7) Calcule as medidas dos ângulos indicados com letras:
PARALELOGRAMOS
Paralelogramo é o quadrilatero que tem os lados opostos paralelos
tipos de paralelogramos
Retangulo - Possui quatro ângulos retos
Losango - Possui os quatro lados congruentes.
Quadrado - Possui os qutro lados congruentes e os quatro ângulos retos
note que:
- todo o quadrado é um losango
- todo quadro é um retângulo
TEOREMA
Os ângulos opostos de um paralelogramo são congruentes.
Prova:
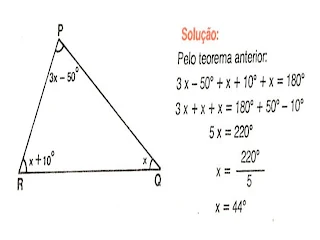
Exercicios Resolvidos
9) Determine as medidas de x, y e z no paralelogramo abaixo:
Solução:
a) Pelo teorema anterior : x = 50°
b) y + 50° = 180° ( os ângulos não opostos são suplementares)
----y = 180° - 50°
----y = 130°
c) Pelo teorema anterior: z = 130°
2) Calcule o valor de x no paralelogramo abaixo:
10) Observe a figura e calcule as medidas de x,y,z e w
11) Baseado nos resultados do exercícios anteriores, responda:
Os ângulos opostos de um paralelogramo são congruentes?
12) Calcule os ângulos indicados nos paralelogramos seguintes:
13) Calcule o valor de x nos paralelogramos abaixo:
14) Calcule o valor de x nos paralelogramos abaixo:























 Os 35 andares da torre são distribuídos da seguinte forma: do segundo ao 16º são andares destinados a espaço para escritórios, do 18º em diante são os pisos reservados ao hotel Hyatt Capital Gate. O primeiro piso e o 17º são plant rooms, salas utilizadas para abrigar máquinas de grande porte, como equipamentos de ar condicionado.
Os 35 andares da torre são distribuídos da seguinte forma: do segundo ao 16º são andares destinados a espaço para escritórios, do 18º em diante são os pisos reservados ao hotel Hyatt Capital Gate. O primeiro piso e o 17º são plant rooms, salas utilizadas para abrigar máquinas de grande porte, como equipamentos de ar condicionado. A edificação é sustentada por um exoesqueleto de aço conhecido por diagrid. Utilizado na construção de grandes edifícios de aço, o diagrid cria estruturas triangulares com vigas diagonais de suporte. A vantagem dessa técnica é que ele requer menos aço estrutural do que uma edificação convencional, já que dispensa a necessidade de pilares e vigas internas.
A edificação é sustentada por um exoesqueleto de aço conhecido por diagrid. Utilizado na construção de grandes edifícios de aço, o diagrid cria estruturas triangulares com vigas diagonais de suporte. A vantagem dessa técnica é que ele requer menos aço estrutural do que uma edificação convencional, já que dispensa a necessidade de pilares e vigas internas.