“Divisão e Conquista: é uma técnica valiosa usada em momentos complicados, onde dividimos um grande problema em problemas menores até ser resolvido". Anatolii Karatsuba
quarta-feira, 16 de setembro de 2015
Exercícios sobre contas de divisão
A operação da divisão é extramente ligada à multiplicação. Dizemos que uma é o inverso da outra. Mas você sabe realizar a divisão? E qual a relação da divisão com a multiplicação?
Vamos fazer alguns exemplos e tentaremos responder a essa pergunta!
Primeiramente, precisamos saber que cada elemento da divisão possui um nome. No exemplo, temos o cálculo de “dez dividido por três” (ou 10 : 3), utilizando oalgoritmo da divisão:
Os termos da divisão são: dividendo, divisor, quociente e o resto
Vamos tentar realizar o cálculo de 125 : 5. Primeiro, analisaremos os elementos do dividendo, respondendo às perguntas:
- 1 é maior que 5? Não!
- 12 é maior que 5? Sim!
Como o doze é maior que o cinco, vamos procurar um número que, multiplicado por 5, chegue próximo ao 12. Vejamos os múltiplos de 5:
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
O resultado 15 é maior do que 12, então ele não nos serve. Vamos utilizar o 5 x 2 = 10.
Ao multiplicar 5 por 2, obtivemos 10 como produto. Esse foi o valor que mais se aproximou do 12 que está no dividendo
Ao subtrair 10 de 12, obtivemos o resto 2. Para continuarmos nossa divisão, nós devemos descer o número 5 (aquele do dividendo) e colocá-lo ao lado do dois, formando 25. Vamos então repetir o processo: qual é o número que multiplicado por cinco aproxima-se de 25? Vejamos:
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
O 5x5 é exatamente o número que estávamos procurando. Basta concluir nossa divisão:
Nós multiplicamos 5 por 5 e obtivemos o produto 25. Esse valor era o que procurávamos
Como o resto da divisão foi zero, dizemos que está é uma divisão exata. Se quisermos verificar se nossa divisão está correta, podemos multiplicar o quociente pelo divisor, isto é, 25 x 5 = 125. O resultado deve ser exatamente o dividendo, no caso 125. Esse processo é conhecido como a prova real da divisão.
Vejamos algumas outras divisões. Quando o resto da divisão não for zero, dizemos que a divisão é inexata ou, simplesmente, que a divisão não é exata.
133 dividido por 13 e 478 dividido por 4 não são divisões exatas, enquanto 150 dividido por 5 é exata
Exercícios:
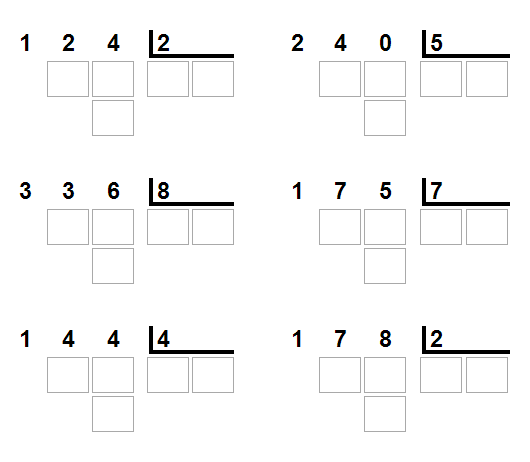
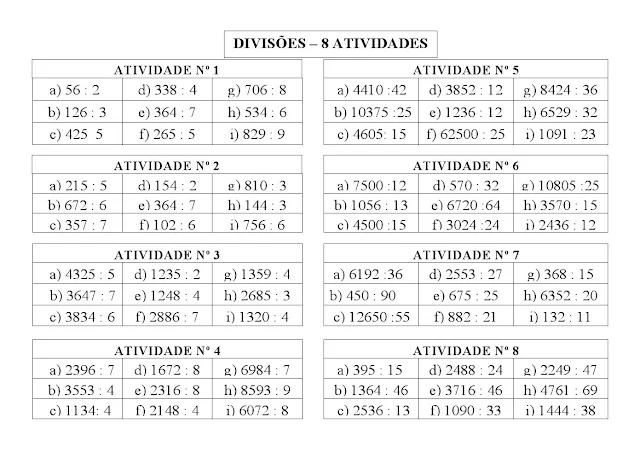
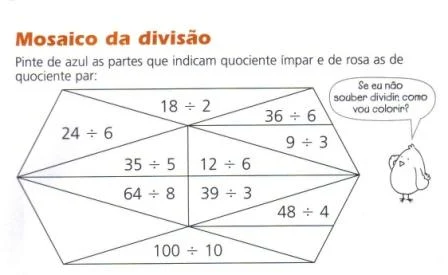
.jpg)
(Fonte:http://www.escolakids.com/)
Exercícios sobre contas de Adição
A adição é a operação responsável por unir os elementos. Por exemplo:
Pedro possui 5 bolas de gude e ganhou mais 3 num jogo com seu colega. Com quantas bolas de gude Pedro ficou?
Pedro possui 5 bolas de gude e ganhou mais 3 num jogo com seu colega. Com quantas bolas de gude Pedro ficou?
Como Pedro tinha 5 bolas de gude e ganhou 3, a operação feita para saber com quantas bolas de gude ele ficou é a da adição: 5 + 3 = 8. Portanto, Pedro ficou com 8 bolas de gude.
Exercícios
1 – Arme e efetue as seguintes adições
a) 112 + 105 =
b) 252 + 298 =
c) 154 + 629 =
d) 898 + 129 =
2 – Resolva os seguintes problemas envolvendo adição.
a) Em uma caixa há 126 laranjas e 269 peras. Quantas frutas há na caixa?
b) Para comemorar o aniversário de Paulo, sua mãe comprou 160 latinhas de refrigerante. Dias antes da festa o avô de Paulo comprou mais 145 latinhas de refrigerante sabor laranja. Quantas latinhas de refrigerante foram compradas para o aniversário de Paulo?
c) Durante o ano, Caio conseguiu juntar o valor de R$ 327,00 através das mesadas que recebe. Caio também ganhou de seu tio o valor de R$ 125,00. Quanto Caio tem em dinheiro?
Exercícios sobre contas de multiplicação
A operação da multiplicação nada mais é do que uma grande soma de parcelas. Logo que começamos a fazer algumas “continhas de vezes”, passamos a aplicar as propriedades da multiplicação sem perceber sua utilização. Que tal nos lembrarmos dos termos da multiplicação? Eles são conhecidos como fator e produto:
Os números que são multiplicados são chamados de fatores e o resultado da multiplicação é chamado de produto
1ª) Propriedade Comutativa
A Propriedade Comutativa garante que, em uma multiplicação, a ordem dos fatores não altera o produto. Vejamos um exemplo:
3 x 9 = 27
9 x 3 = 27
Na multiplicação, nós podemos trocar os fatores de posição, mas o resultado da operação da multiplicação será o mesmo, não importa qual número queremos multiplicar primeiro. Por exemplo, se quisermos multiplicar quatro números, podemos escolher a ordem que preferirmos, o resultado nunca mudará! Vamos ver outro exemplo:
1 x 2 x 3 x 4 = 24
2 x 3 x 4 x 1 = 24
3 x 4 x 1 x 2 = 24
4 x 2 x 3 x 1 = 24
2ª) Propriedade do Elemento Neutro
A propriedade do elemento neutro garante que existe um número que, ao ser multiplicado por qualquer outro número, não o altera. Isso mesmo, qualquer número multiplicado pelo elemento neutro não muda! Você sabe que número é esse? É o número 1! Por essa razão, o número 1 é conhecido como o elemento neutro da multiplicação. Vamos ver alguns exemplos:
1 x 2 = 2
10 x 1 = 10
15 x 1 = 15
1 x 12.345 = 12.345
3ª) Propriedade do Elemento Nulo
A propriedade do elemento nulo lembra a última propriedade que vimos. Segundo essa propriedade, sempre que multiplicarmos qualquer número pelo elemento nulo, o resultado será zero! Você sabe quem é o elemento nulo? É o próprio zero Qualquer número multiplicado por zero sempre terá o produto igual a zero. Veja os exemplos a seguir:
2 x 0 = 0
0 x 5 = 0
7 x 0 x 2 = 0
4ª) Propriedade Associativa
Quando multiplicamos três ou mais fatores, podemos escolher várias ordens para resolver a operação da multiplicação, e o resultado sempre será o mesmo. Vejamos de quais maneiras podemos resolver a multiplicação 3 x 5 x 7:
(3 x 5) x 7 = 15 x 7 = 105
3 x (5 x 7) = 3 x 35 = 105
5 x (3 x 7) = 5 x 21 = 105


(Fonte: escolakids.com.br)
Estudando a tabuada

|
Como desenvolver o cálculo mental
Alguns procedimentos de cálculo mental
Na adição: Calcular primeiro dezenas exatas e os números que formam dezenas.
Na subtração : Arredondar e depois fazer a compensação.
Decompor o subtraendo (valor que será subtraído).
Alterar o minuendo para evitar o "empresta um".
Agrupar as parcelas em unidades, dezenas e centenas.
Explorar a idéia da adição. Ex.: 400 - 160. Quanto falta em 160 para chegar a 400? Para 200 faltam 40; de 200 para 400 faltam 200. A resposta é 240.
Na multiplicação :Decompor um dos fatores.
Na multiplicação :Decompor um dos fatores.
Na divisão: Fazer simplificações sucessivas:
Para memorizar alguns resultados
Dominó Jogos ajudam a aprimorar a capacidade de cálculo. Para a turma ficar craque nasoma de parcelas com resultado até 6, por exemplo, leve para a classe um dominó comum e estabeleça uma regra diferente: os jogadores devem unir as peças de forma que a soma das duas seja 6.
Crachá Distribua crachás com números de 0 a 10 para todos as crianças antes do recreio. Na volta, peça que entrem na sala em duplas de forma que a soma de seus crachás seja 10. Em outra atividade, varie os números dos crachás e crie novas senhas.
- Pares com soma par.
- Pares com soma ímpar.
- A divisão dos dois números é exata.
- Número escrito em um crachá é o dobro do outro.
Dominó Jogos ajudam a aprimorar a capacidade de cálculo. Para a turma ficar craque nasoma de parcelas com resultado até 6, por exemplo, leve para a classe um dominó comum e estabeleça uma regra diferente: os jogadores devem unir as peças de forma que a soma das duas seja 6.
Crachá Distribua crachás com números de 0 a 10 para todos as crianças antes do recreio. Na volta, peça que entrem na sala em duplas de forma que a soma de seus crachás seja 10. Em outra atividade, varie os números dos crachás e crie novas senhas.
- Pares com soma par.
- Pares com soma ímpar.
- A divisão dos dois números é exata.
- Número escrito em um crachá é o dobro do outro.
(Fonte:http://revistaescola.abril.com.br/)
Exercícios sobre contas de Subtração
Em geral, é mais difícil as crianças identificarem a presença da subtração nos problemas.
Qual será a razão dessa dificuldade? A razão está no fato de que, geralmente, associamos a subtração apenas ao ato de retirar, mas há outras duas situações que também estão relacionadas com a subtração: os atos de comparar e de completar.
Vamos exemplificar cada uma das três situações:
Problema que envolve o ato de retirar
Problema que envolve comparação
Problema que envolve a ideia de completar


(Fonte: novaescola e educax.blogspot.com.br)
O Cálculo algorítmico
É essencial ensinar o que está por trás do passo a passo das contas armadas
O algoritmo garante chegar ao resultado baseado em um número finito de passos
São vários os tipos de conta armada que existem para somar e subtrair. O jeito mais comum no Brasil é o cálculo com recurso à ordem superior, com reserva (adição) ou com empréstimo (subtração): o famoso "vai um" e "empresta um", ações correspondentes às decomposições numéricas.
Quando bem compreendido pela turma, o algoritmo é um meio poderoso para realizar cálculos com resultados precisos, quando não se quer privilegiar a reflexão sobre cada etapa de um problema.
Expectativas de aprendizagem
Os Parâmetros Curriculares Nacionais estabelecem que ao final do 3º ano os alunos devem:
• Desenvolver procedimentos de cálculo - mental, escrito, exato, aproximado - pela observação de regularidades e de propriedades das operações e pela antecipação e verificação de resultados.
• Utilização de sinais convencionais (+, -, x, :, =) na escrita das operações.
As Orientações Curriculares do Município de São Paulo trazem as propostas divididas pelos anos.
Para o 2º ano:
• Utilizar sinais convencionais (+,-, =) na escrita de operações de adição e subtração.
Para o 3º ano:
• Utilizar uma técnica convencional para calcular o resultado de adições.
• Utilizar uma técnica convencional para calcular o resultado de subtrações, sem recurso à unidade de ordem superior (sem "empréstimos").
portaldoprofessor.mec.gov.br/fich
Exercícios sobre Adição e Subtração de matrizes
É uma tabela com m.n elementos dispostos em m linhas e n colunas.
Adição e Subtração de Matrizes
1)Dadas as matrizes, e, determine a matriz D resultante da operação A + B – C.
Para a resolução desse exercício, você terá que fazer a adição do elemento da PRIMEIRA linha e PRIMEIRA coluna da MATRIZ A com o elemento da PRIMEIRA linha e PRIMEIRA coluna da MATRIZ B e subtrair com o elemento da MATRIZ C e assim por diante.
Resolução:
Exercícios:
1)Os elementos de uma matriz M quadrada de ordem 3 x 3 são dados por aij, onde:
i + j, se i ≠ j
0, se i = j
Determine M + M.
2)Determine a matriz C, resultado da soma das matrizes A e B.
3)Determine a matriz resultante da subtração das seguintes matrizes:
4)Determine a matriz resultante da adição das seguintes matrizes:
5)Determine a matriz resultante da subtração das seguintes matrizes:
(fonte:http://comocalcular.com.br/exercicios/matrizexerciciosresolvidos)
Exercícios sobre logaritmos
Definição de Logaritmo
Pode-se definir logaritmo da seguinte forma:
Ou seja, o logaritmo é o expoente que uma certa base deve ter para produzir um número determinado (no nosso caso o N).
a - Base
N - Logaritmando
x - Logaritmo
A segunda vem simplesmente do fato que um número elevado a um é igual a ele mesmo.
A terceira vem aplicando a definição em "a" elevado a "n".
A quarta é só aplicar a definição no logaritmo de "x" na base "a".
Agora vejamos algumas das propriedades dos logaritmos.
O logaritmo do produto de dois números é igual à soma do logaritmo de cada número.
O logaritmo do quociente de dois números é igual ao logaritmo do dividendo (número de cima) subtraído (menos) o logaritmo do divisor (número de baixo).
Uma das consequências dessa propriedade é a seguinte. Neste caso o dividendo é 1 (um). Como o logaritmo de um é zero, sobra apenas o negativo do logaritmo do divisor.
O logaritmo de um número elevado a "n" é igual a "n" vezes o logaritmo do número.
Desta forma temos as seguintes consequências: O que significa também que:
a)424
Nomenclatura
Quando utilizamos o logaritmo cada um dos termos tem um nome. Neste caso temos:a - Base
N - Logaritmando
x - Logaritmo
Consequências da definição
Com base na definição podemos facilmente chegar as seguintes consequências: A primeira vem do fato que qualquer número real (diferente de zero) elevado a 0 (zero) é igual a 1 (um).A segunda vem simplesmente do fato que um número elevado a um é igual a ele mesmo.
A terceira vem aplicando a definição em "a" elevado a "n".
A quarta é só aplicar a definição no logaritmo de "x" na base "a".
Agora vejamos algumas das propriedades dos logaritmos.
Logaritmo de um produto
O logaritmo do produto de dois números é igual à soma do logaritmo de cada número.
Logaritmo de um quociente
O logaritmo do quociente de dois números é igual ao logaritmo do dividendo (número de cima) subtraído (menos) o logaritmo do divisor (número de baixo).
Uma das consequências dessa propriedade é a seguinte. Neste caso o dividendo é 1 (um). Como o logaritmo de um é zero, sobra apenas o negativo do logaritmo do divisor.
Logaritmo de uma potência
O logaritmo de um número elevado a "n" é igual a "n" vezes o logaritmo do número.
Mudança de base
Quando se tem um logaritmo em uma determinada base e conhecemos o logaritmo do logaritmando e da base em outra base, podemos fazer uma mudança da seguinte forma: Assim o logaritmo se torna um quociente do logaritmando e da base em uma nova base "a".Desta forma temos as seguintes consequências: O que significa também que:
- (FUVEST - 2012)1)Tendo em vista as aproximações log10 2 ≅ 0,3 e log10 3 ≅ 0,48 então, o maior número inteiro n que satisfazendo 10n ≤ 12418, é igual a:
b)437
c)443
d)451
e)460
2) Calcule o Log24 6 sabendo que o Log27 6 = x que o Log27 4 = y.
3) (UFRGS) Se  e
e  , então
, então  é
é
(A) 
(B)
(B)
(C)
(D) 
(E) 
4) Calcule o valor dos seguintes logaritmos:
| a) | b) |
| c) | d) |
| e) | f) |
| g) | h) |
5) Calcule o valor da incógnita "N" em cada exercício, aplicando a equivalência fundamental:
| a) | b) | c) | d) |
((http://www.matematiques.com.br/e http://delta-y.blogspot.com.br/http://tudodeconcursosevestibulares.blogspot.com.br/)
Assinar:
Comentários (Atom)
Destaque!!!!!!!!!!!
Aula criativa de matemática sobre a conversão do dólar
Um emprego em um navio de cruzeiro pode ser uma grande chance de conhecer lugares novos e ganhar um bom salário. Quanto melhor for seu ingl...

-
O objeto capaz de medir o valor de um ângulo é chamado de transferidor, podendo ele ser de “meia volta” (180º) ou volta inteira (360º). ...
-
Frações: Própria, imprópria, aparente e números mistos. Temos que ter a noção básica de que toda fração é uma divisão. E que uma f...
-
A potenciação é uma multiplicação de fatores iguais Exemplos: 1) (1,2)² = 1,2 x 1,2 =1,44 2) (0,4)³ = 0,4 x 0,4 x 0,4 = 0,064 vamo...











