As derivadas podem ser usadas para representar tudo, desde a variação de taxas de juros até taxas em que peixes morrem e moléculas de gás se movimentam, elas têm implicações em todas as ciências.Outro exemplo é no caso de encher um recipiente com água. Sabendo a função que descreve o formato do recipiente e a quantidade de água que entra em determinado tempo, descobrimos a velocidade que a água cairá.
Encontramos derivadas também no comportamento da função de ondas estacionárias presentes nos sons de instrumentos musicais e de todos os tipos de sons.
A derivada pode ser interpretada geometricamente como a inclinação de uma curva e, fisicamente, como uma taxa de variação.
A operação primária do cálculo diferencial é encontrar a derivada de uma função. Na tabela a seguir, supomos que  e
e  são funções deriváveis em
são funções deriváveis em  e
e  é um número real. Essas fórmulas são suficientes para derivar qualquer função elementar.
é um número real. Essas fórmulas são suficientes para derivar qualquer função elementar.
 e
e  são funções deriváveis em
são funções deriváveis em  e
e  é um número real. Essas fórmulas são suficientes para derivar qualquer função elementar.
é um número real. Essas fórmulas são suficientes para derivar qualquer função elementar.
Precisamos estar cientes de que a Derivada é uma propriedade local da função, isto é, para um determinado valor de x. Por isso não podemos envolver toda a função. Observe o gráfico a seguir, ele demonstra a intersecção entre uma reta e uma parábola, função do 1º grau e função do 2º grau respectivamente:
A reta consiste na derivação da função da parábola.
Vamos determinar as variações de x quando aumenta ou diminui seus valores. Considerando que e x varia de x = 3 para x = 2, achar ∆x e ∆y.
∆x = 2 – 3 = –1

Agora vamos determinar a derivada da função y = x² + 4x + 4.
y + ∆y = (x + ∆x)² + 4(x + ∆x) + 4 – (x² + 4x + 4)
= x² + 2x∆x + ∆x² + 4x + 4∆x + 4 – x² – 4x – 4
= 2x∆x + ∆x² + 4∆x
A derivada da função y = x² + 4x + 8 é a função y’ = 2x + 4. Observe o gráfico:
| A derivada é o coeficiente angular da reta tangente ao gráfico da função no ponto x0. |
A derivada de uma função y = f(x), pode ser representada também pelos símbolos:
y' , dy/dx ou f ' (x).
y' , dy/dx ou f ' (x).
A derivada de uma função f(x) no ponto x0 é dada por:
Regras de derivação:

Derivadas essenciais:
Regra nº 1: (k' = 0) - Derivada de uma constante:
Segundo a regra assume-se k como sendo uma constante, simplificando; uma constante é um número qualquer (pertencente a qualquer dos conjuntos de números).
Exemplo:

A derivada de uma constante (k) é sempre igual a 0.
Regra nº 2: (x' = 1) - Derivada de x:
Assume-se x como a variável de uma função; em uma função a variável poderá ser definida por outra letra qualquer normalmente é usada a letrax.
Exemplo:

A derivada da variável (usualmente X) é sempre igual a 1.
Regra nº 3: (k . x' = k) - Derivada de uma constante multiplicada por x:
A derivada da multiplicação entre uma constante e a váriavel x é igual a própria constante como se pode verificar no exemplo abaixo onde é utilizada a regra nº 7 (derivada da multiplicação).
Exemplo:

A derivada de uma Constante vezes X é sempre igual a Constante.
Nota: Atenção aos casos em que x apresenta um grau maior que 1 quando assim for a regra a utilizar será a regra nº4.
Regra nº 9: (k' = 0) - Derivada da potência de base x:
Alpha é igual ao grau da função derivada, repare que o grau da potência decrescence sempre em -1 relativamente a potência inicial.
 Exemplo:
Exemplo:

A derivada da potencia de base X é sempre igual ao grau da potência inicial, multiplicado pela base cujo grau decresce em -1 unidade.
Exercícios:
1. Calcule a derivada da função exponencial: 

Desta forma, iremos mostrar ou explicar como resolver as derivadas indo diretamente a fórmula ou regras necessárias.


Exemplo:

A derivada da multiplicação entre uma constante e a váriavel x é igual a própria constante como se pode verificar no exemplo abaixo onde é utilizada a regra nº 7 (derivada da multiplicação).





Regra da soma

Regra da subtração

Regra da multiplicação por um escalar
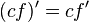
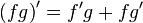
 sendo esta válida para todo
sendo esta válida para todo  no domínio das funções com
no domínio das funções com  .
.
onde 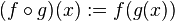 é a composição de
é a composição de  com
com  . Sendo esta válida para
. Sendo esta válida para  no domínio da função
no domínio da função  e tal que
e tal que  esteja no domínio da função
esteja no domínio da função  .
.
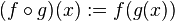 é a composição de
é a composição de  com
com  . Sendo esta válida para
. Sendo esta válida para  no domínio da função
no domínio da função  e tal que
e tal que  esteja no domínio da função
esteja no domínio da função  .
.
(fonte: brasilescola entre outros)







Nenhum comentário:
Postar um comentário